Ayuda con el siguiente estudio de funciones
Hola, necesito ayuda para resolver este ejercicio de aplicación de la derivada para el estudio de funciones
Dada f(x)=2- |x^5-1|, analizar intervalos de crecimiento y decrecimiento, extremos relativos, concavidad y puntos de inflexión
Un saludo
1 Respuesta
Respuesta de Lucas m
1
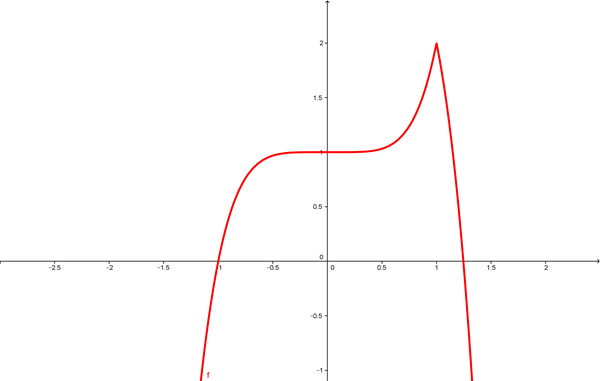
y=2-|x^5-1| es una función a trozos:
x^5-1>0 si x>1 entonces |x^5-1|=x^5-1
x^5-1<0 si x<1 entonces |x^5-1|=-x^5+1
$$\begin{align}&y=2-(1-x^5)=1+x^5 \ si x<1\\ &\\ &y=2-x^5+1=3-x^5 \ si \geq1\\ &\\ &En \ x=1 \ la \ función \ es \ continua\\ &\lim_{ x \to \ 1^-}1+x^5=1+1=2\\ &\\ &\lim_{ x \to \ 1^+}3-x^5=3-1=2\\ &\\ &Corta al eje OY \ x=0 \Rightarrow\ y=1\\ &\\ &Corta \ al\ eje \ OX \ y=0 \Rightarrow \\ &3-x^5=0 \Rightarrow x=\sqrt[5]{3}\\ &1+x^5=0 \Rightarrow x=1\\ &\\ &y'=5x^4 \ si \ x<1\\ &y'=-5x^4 \ si \ x>1\\ &\\ &No \ es \ derivable \ en \ x=1\\ &y'(1^-)=5\\ &y'(1^+)=-5\\ &En punto (1,f(1))=(1,2) \ es \ un\ "pico"\\ &\\ &Crecimiento y'=0 \ 5x^4=0 \Rightarrow x=0\\ &-5x^4=0 \Rightarrow x=0 \\ &Intervalos \ crecimiento \ cogemos \\ &\ puntos \ críticos(y'=0)\Rightarrow x=0\\ &puntos \ no \ derivables \ x=1\\ &(-\infty,0)\ y'(-10)=5(-10)^4>0\ creciente\\ &(0,1) \ y'(1/2)=5(1/2)^4>0 \ creciente\\ &En \ x=0 \ no \ cambia \ el \ crecimiento\Rightarrow Punto de Inflexión \ con \ tangente \ horizontal\\ &(1,+\infty) \ y'(10)=-5(10)^4<0\ decreciente\\ &\\ &Concavidad:\\ &\\ &y''=20x^3 \ si \ x<1\\ &y''=-20x^3 \ si\ x>1\\ &\\ &y''=0\Rightarrow x=0\\ &\\ &Intervalos \ concavidad-convexidad:\\ &(-\infty,0) \ y''(-10)=20(-10)^3<0(hacia \ abajo)\\ &(0,1) \ y''(1/2)=20(1/2)^3>0(hacia \ arriba)\\ &(1,+\infty) \ y''(10)-20(10)^3<0(hacia \ abajo)\\ &En \ x=1\ cambia \ la \ concavidad\ pero \ no \ se \ considera \ P I\ al \ no \ ser \ derivable\end{align}$$La gráfica
