Valores máximos y mínimos, puntos de inflexión, los intervalos de crecimiento y decrecimiento y los de concavidad
Dada la función y=(x2-x-1)2, utiliza el criterio de la primera derivada para obtener:
1.- Valores máximos y mínimos.
2.- Puntos de inflexión.
3.- Intervalos de crecimiento y decrecimiento.
4.- La concavidad

Reescribiré la función para estar seguros que hablamos de la misma función:
$$\begin{align}&f(x) = (x^2-x-1)^2\\&Calculemos \ f'(x) \ y \ f''(x)\ que\ las \ vamos\ a \ necesitar\\&f'(x) = 2(x^2-x-1)(2x-1)\\&f''(x) = 2\Big((2x-1)(2x-1)+(x^2-x-1)2 \Big) =2\Big((2x-1)^2+2(x^2-x-1) \Big)\\&críticos \ (cuando \ f'(x)=0)\\&\\&f'(x)=0 \Rightarrow \\&x^2-x-1 = 0 \Rightarrow x_1=1,62 \lor x_2=-0,62\\&\lor\\&2x-1=0 \Rightarrow x_3=0,5\\&f''(1,62)>0 \rightarrow minimo\\&f''(-0,62)>0 \rightarrow minimo\\&f''(0,5) <0 \rightarrow maximo\\&Inflexión\ (cuando f''(x)=0)\\&f''(x) = 2\Big((2x-1)^2+2(x^2-x-1) \Big)\\&f''(x)=2(4x^2-4x+1+2x^2-2x-2)=\\&=2(6x^2-6x-1)\\&f''(x)=0 \Rightarrow \\&6x^2-6x-1=0 \Rightarrow\\&x_1=1,15 \lor x_2=-0,15\\&Crecimiento/Decrecimiento (veamos\ f')\\&Antes \ de\ x=-0,62...f'(-1)<0...decrece\\&Entre\ -0,62\ y \ 0,5...f'(0)>0....crece\\&Entre\ 0,5\ y \ 1,62...f'(1) <0...decrece\\&Despues\ de 1,62....f'(2) > 0...crece\\&Luego\\&Crecimiento: (-0,62; 0,5) \cup (1,62; +\infty)\\&Decrecimiento = (- \infty,-0,62) \cup (0,5; 1,62)\\&\end{align}$$
- Compartir respuesta

1 respuesta más de otro experto
·
·
Haremos la primera derivada y luego la segunda.
$$\begin{align}&y=(x^2-x-1)^2\\&\\&y'=2(x^2-x-1)(2x-1)\\&\\&\text{La segunda la igualaremos a 0}\\&\\&y''= 2\left((2x-1)(2x-1)+2(x^2-x-1) \right)=\\&\\&2(2x-1)^2+4(x^2-x-1)=\\&\\&8x^2-8x +2+4x^2-4x-4 =\\&\\&12x^2-12x-2 = 0\\&\\&\text{calculamos las raíces}\\&\\&x=\frac{12\pm \sqrt{144+96}}{24}= \frac{12\pm \sqrt {240}}{24}=\\&\\&\frac{12\pm 4 \sqrt {15} }{24}= \frac{3\pm \sqrt{15}}{6}\end{align}$$Como esas respuestas son muy feas las pondré en decimal para poder escribirlas de forma sencilla
x1 = -0.145497224
x2 = 1.145497224
Tenemos que calcular el signo de la derivada segunda. Como es una parábola con coeficiente director positivo será positiva a los lados y negativa entre las raíces. Si no te sirve este argumento puedes tomar tres puntos de cada intervalo y calculas el valor de la derivada segunda en ellos
(-oo, -0.145497224) f''(x)>0 ==> f(x) es cóncava hacia arriba
(-0.145497224, 1.145497224) f''(x) <0 ==> f(x) es cóncava hacia abajo
(1.145497224, oo) f''(x) >0 ==> f(x) es cóncava hacia arriba
Las palabras cóncava y convexa son inutilizables porque cada país, cada autor, cada libro dicen una cosa distinta. Cóncava hacia arriba es con forma de copa, y cóncava hacia abajo con forma de iglú.
-------
Perdón, enfrascado con la concavidad se me había olvidado lo de máximos, minimos e intervalos de crecimiento y decrecimiento.
La función es
y=(x^2-x-1)^2
Eso significa que es no negativa, luego hallá donde valga 0 tendra mínimos.
Ya vimos que
x1 = -0.145497224
x2 = 1.145497224
eran raíces de x^2-x-1
luego esos dos puntos son mínimos y el valor de la función es 0
El otro punto crítico era 1/2. Si una función es contibua debe tener un máximo entre dos mínimos, pero por si acaso usamos otro criterio, el valor de la derivada segunda es
y''(1/2) = 12(1/2)^2 - 12(1/2) - 2 = 3-6-2 = -5 luego es un máximo relativo
Y el valor de la función en este máximo es
[(1/2)^2 - 1/2 - 1]^2 = (1/4 - 1/2 - 1)^2 = [(1-2-4)/4]^2 =(-5/4)^2 = 25/16
Luego el máximo es (1/2, 25/16)
Y los intervalos de crecimiento decrecimiento teniendo en cuenta que f es un polinomio de grado 4 con coeficiente director positivo, por lo que empieza descendiendo desde infinito son:
(-oo, -0.145497224) decreciente
(-0.145497224, 0.5) creciente
(0.5, 1.145497224) decreciente
(1.145497224, +oo) creciente.
Perdón, la tengo mal, confundí los ceros de la derivada segunda con los de la primera siendo que me faltaban de calcular dos de ellos. Entonces están mal los intervalos de crecimiento y decrecimiento. Perdón por el fallo y puntúa a Gustavo como es debido.
Haz caso a su respuesta mientras corrijo la mía.

¡Gracias!
Espero su corrección, perdón pero le entiendo más a usted, es más explícito, lo felicito, nos ayuda bastante con sus explicaciones. Gracias de nuevo. Saludos
Haremos la primera derivada y la igualaremos a 0 para hallar los puntos críticos. Y la segunda igualada a 0 para hallar los puntos de inflexión.
$$\begin{align}&y=(x^2-x-1)^2\\&\\&y'=2(x^2-x-1)(2x-1)\\&\\&\\&\\&y''= 2\left((2x-1)(2x-1)+2(x^2-x-1) \right)=\\&\\&2(2x-1)^2+4(x^2-x-1)=\\&\\&8x^2-8x +2+4x^2-4x-4 \\&\\&y''=12x^2-12x-2\\&\\&\text{Los puntos críticos son los que }f'(x)=0\\&\\&2x-1=0\implies2x=1\implies\\&x_1=\frac 12\\&\\&x^2-x-1=0\implies x=\frac{1\pm \sqrt{1+4}}{2}\implies\\&x_2=\frac{1-\sqrt 5}{2}\approx -0.618034\\&x_3=\frac{1+\sqrt 5}{2}\approx 1.618034\\&\\&\text {veamos si son máximos o mínimos con }f''(x)\\&\\&f''\left(\frac 12\right)=-5\lt0\implies \text{máximo}\\&f''(-0.618034)=10\gt0\implies \text {mínimo}\\&f''(1.618034)= 10\gt 0\implies \text{mínimo}\\&\\&f(x_2)\; y\; f(x_3)=0 \text{ por ser raíces de }x^2-x-1\\&f(0.5)=1.5625\\&\\&\text{Máximo =}(0.5,\;1.5625)\\&\text{Mínimos=} \{( -0.618034,0), \quad(1.618034,0)\}\\&\\&\text{Puntos de inflexión cuando }f''(x)=0\\&\\&12x^2-12x-2=0\\&\\&x=\frac{12\pm \sqrt{144+96}}{24}=\frac{3\pm \sqrt{15}}{6}\\&\\&x_{i_1}\approx -0.145497\\&x_{i_2}\approx 1.145497\\&\\&f(-0.145497) =f(1.145497)=0.694445\\&\\&\text{Puntos de Inflexión:}\\&(-0.145497,\;0.694445)\\&(1.145497,\;0.694445)\\&\\&\end{align}$$Salgamos del editor de ecuaciones que en él no se pueden escribir reflexiones profundas. Ya hemos calculado los mínimos, máximos y puntos de inflexión.
Ahora los intervalos de crecimiento o decrecimiento se pueden calculan mediante el signo de la derivada primera, esto se puede hacer evaluando puntos entre las raíces de esa derivada, o conociendo cómo se comporta la derivada. Y tambíen se pueden calcular sabiendo que donde hay un mínimo antes es decreciente y luego creciente y donde hay un máximo antes crece y después decrece.
Usaré este último. Como en x= -0.618034 hay mínimo antes decrece y luego crece hasta el maximo en x=0.5 y luego decrece hasta 1.618034 donde hay un mínimo y después crece hasta infinito.
Y para la concavidad se calcula el signo de la derivada segunda, aquí usaré que
f ''(x) = 12x^2 - 12x-2
Es un polinomio de grado 2 con signo positivo en x^2, luego es positiva a la izquierda y derecha de las raíces y negativa entre ellas. Cuando sea positiva diré que la función es cóncava hacia arriba y cuando sea negativa es cóncava hacia abajo. Es inútil intentar entenderse con las palabras cóncava y convexa, cada país, cada libro, cada autor dice una cosa distinta sobre lo que es una cosa y otra.
Cóncava hacia arriba es en forma de U y cóncava hacia abajo en forma de iglú.
Pues con todo este rollo queda que los intervalos son:
$$\begin{align}&(-\infty,\;-0.618034) \text{ decreciente}\\&(-0.618034,\;0.5)\text{ creciente}\\&(0.5,\;1.618034) \text{ decreciente}\\&(1.618034,\;\infty) \text{ creciente}\\&\\&\text{Y los de concavidad son:}\\&(-\infty,\;-0.145497) \text{ Cóncava hacia arriba}\\&(-0.145497,1.145497)\text{ Cóncava hacia abajo}\\&(1.145497,\infty)\text{ Cóncava hacia arriba}\end{align}$$Y finalmente nada mejor que una gráfica:
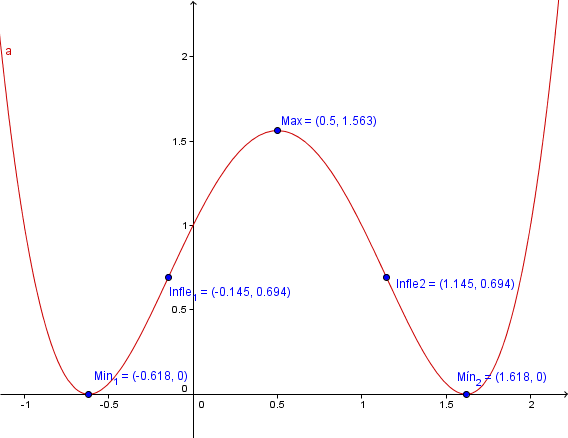
- Compartir respuesta

¿Cuando escribes tantas líneas seguidas con el editor no te va el ordenador que no puede y escribes y tarda mucho en aparecer en pantalla? Saludos. - Valero Angel Serrano Mercadal
Si, pero como en este momento estoy haciendo esto desde un lugar que no es mi lugar habitual, la verdad que no sabía si era tema del editor o del lugar donde me encontraba. Igualmente reconozco que a este editor le falta bastante para ser considerado "bueno", incluso la ayuda que ellos mismos proporcionan incluye instrucciones que el editor no las soporta. Saludos! - Anónimo
Yo creo que es un editor que consume muchísimos recursos. Tengo un I3 que no es moco de pavo y cuando he escrito 5 líneas ya se empieza a notar que le cuesta trabajo escribir o mover los cursores y llega un momento que se hace un martirio escribir. Y, o yo no sé cómo o no muestra dos matrices a la vez, luego de operaciones de álgebra nada. - Valero Angel Serrano Mercadal
No contestes la pregunta de María Teresa Sanchez hasta que no puntué, tiene muchas pendientes conmigo. Saludos - Valero Angel Serrano Mercadal
Uh, olvidé verificar eso y ya había respondido. Lo tengo en cuenta para las próximas... - Anónimo