Tengo esta duda con este problema de calculo
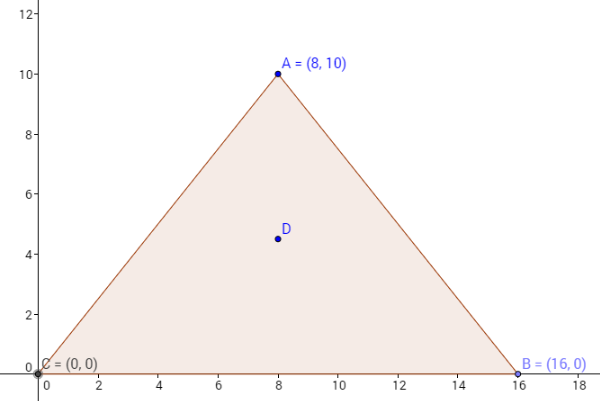
Tres ciudades están situadas en los vértices de un triángulo isósceles. Las ciudades B y C
que distan entre sí 16 millas están situadas en la base, en tanto que A es el tercer vértice y
a una distancia de 10 millas de la base. ¿A que distancia de A sobre la altura del triángulo,
se debe ubicar una instalación de bombeo de manera que se emplee la menor longitud de
cañerías para abastecer de agua a las tres ciudades?
2 respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta
1


Profe, en la primer reescritura de la ecuación se olvidó el cuadrado que está con el 8. - Anónimo