Inecuación racional y plinomica. La necesito con urgencia

Hagamos todo siguiendo tu símbolo, sabiendo que en realidad será mayor o igual (o menor o igual si en algún momento cambia.

Asumo que lo básico lo conocés (si no es así comenta)

$$\begin{align}&{4x^2+3\over x} \ge {2x+1 \over 2-x}\\&(Si \ x>2,\ multiplico\ por\ 2-x\ invirtiendo\ la\ igualdad\ ( \alpha))\\&{(4x^2+3)(2-x)\over x} \le 2x+1\\&(Como \ x>2,\ multiplico\ por\ x (manteniendo\ el\ signo))\\&(4x^2+3)(2-x)\le (2x+1)x\\&(Cuentas)\\&8x^2-4x^3+6-3x\le 2x^2+x\\&(Sumas\ y\ restas\ no\ afectan\ la\ igualdad)\\&0 \le -8x^2+4x^3-6+3x+ 2x^2+x\\&(Reordenando...)\\&0 \le +4x^3-6x^2+4x-6\\&(Analizando\ un\ poco\ se\ ve\ que \ 1,5\ es \ raiz)\\&0 \le (x-1.5)(4x^2+4)\\&(las\ otras\ raices\ son\ imaginarias (\pm i))\\&Juntando\ \alpha\ y\ esto,\ x>2\\&\\&Por\ \alpha,\ queda\ ver\ cuando\  \ x<2\\&(Si \ x<2,\ multiplico\ por\ 2-x\ manteniendo\ la\ igualdad\ ( \beta))\\&{(4x^2+3)(2-x)\over x} \ge 2x+1\\&Se\ abre\ una\ nueva\ rama\ (x>0) (\gamma)\\&(4x^2+3)(2-x) \ge (2x+1)x\\&Llegamos\ a \ lo\ mismo\ que\ antes\ pero\ con\ la\ igualdad\ para\ el\ otro\ lado\\&0 \ge (x-1.5)(4x^2+4)\\&(las\ otras\ raices\ son\ imaginarias (\pm i))\\&Pero\ x<2\ así\ que\ no \ hay\ solucion de\ este\ lado\\&\therefore \\&x>2 \\&\\&\\&\\&\\&\\&\\&\end{align}$$

$$\begin{align}& \end{align}$$

¡Hola Duberneyrios!

·

$$\begin{align}&\frac{4x^2+3}x \gt \frac{2x+1}{2-x}\\&\\&\text{Es importante separar los casos}\\&\text{según el signo de x  y (2-x)}\\&\\&x\in(-\infty,0)\implies x\lt0,\quad(2-x)\gt0\\&\\&x\in (0,2)\implies x\gt0,\quad (2-x)\gt0\\&\\&x\in(2,\infty)\implies x\gt 0,\quad(2-x)\lt0\\&\\&\text{al pasar los denominadores al otro lado}\\&\\&(4x^2+3)(2-x)\;\#\;x(2x+1)\\&\\&\text{# Será < ó > no nos importa de momento.}\\&\text{Se mantiene la desigualdad si hay 0 o 2}\\&\text{denominadores negativos, cambia si hay 1}\\&\\&(4x^2+3)(2-x)\;\#\;x(2x+1)\\&\\&8x^2-4x^3+6-3x-2x^2-x\; \#\;0\\&\\&-4x^3+6x^2-4x+6\;\#\;0\\&\\&\text{Se han pasado con la ecuación}\\&(1.5-x)(4x^2+4)\#0\\&\\&\text{El segundo factor es siempre positivo}\\&\text{luego no afecta al signo}\\&1.5-x\; \#\;0\\&\\&1.5\;\#\;x\\&\\&\text{Y ahora vamos ya con los tres casos:}\\&\\&1)\quad x\in(-\infty,0)\implies x\lt0,\quad(2-x)\gt0\\&\text{hay un negativo y un positivo, cambia el signo original}\\&1.5\lt x\\&\text{pero como }\\&x\lt0\\&\text{no hay solución}\\&\\&2)\quad x\in (0,2)\implies x\gt0,\quad (2-x)\gt0\\&\text{ningún negativo, se conserva el signo original}\\&1.5\gt x\\&\text{como debe eser }0\lt x\lt 2\\&x\in(0,\;1.5)\\&\\&3) x\in(2,\infty)\implies x\gt 0,\quad(2-x)\lt0\\&\text{hay un negativo, # será el signo original cambiado}\\&1.5 \lt x\\&\text{pero como debe ser }x\gt 2\\&\text{no hay solución en el tercer caso}\\&\\&\text{Luego la única solución es:}\\&\\&0\lt x\lt1.5\end{align}$$

En casos como este hay que hacer una gráfica para comprobar, es fácil confundirse.

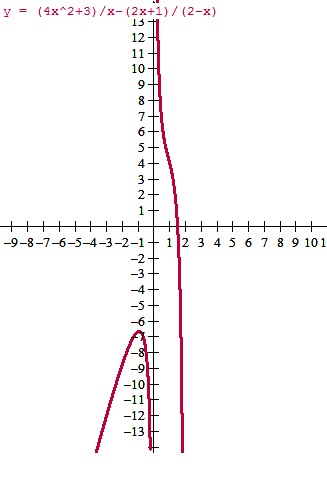
Y la gráfica demuestra que está bien, la función graficada cumple la desigualdad cuando es positiva, entre 0 y 1.5