Cual es el valor de la siguiente integral
Espero y me puedan ayudar
Cual es el resultado de la siguiente integral utilizando el método de integración por partes.
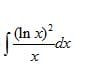
Su información seria de gran ayuda
2 Respuestas
Esta integral no se hace por partes. Se hace con un cambio de variable:
$$\begin{align}&\int \frac{(lnx)^2}{x}dx=\\&\\&lnx=t \Rightarrow dt=\frac{1}{x}dx\\&\\&=\int t^2 dt= \frac{t^3}{3}=\frac{ln^3x}{3}+C\end{align}$$Yo la haría así
·
Yo esta integral no la haría por partes sino por cambio de variable. Pero como ya vi antes que la integral de coseno al cuadrado estaba puesta para hacer por partes, y nunca se hace por partes, voy a suponer que esta se pueda hacer, voy a ver
$$\begin{align}&I=\int \frac{(ln\, x)^2}{x}dx=\\&\\&u=(ln\,x)^2\quad\quad du = 2\,ln\,x·\frac {dx}{x}\\&\\&dv = \frac {dx}{x} \quad\quad v=lnx\\&\\&=(ln\,x)^3 - 2\int \frac{(ln\,x)^2}{x}dx =\\&\\&\text{¡Qué curioso! a la primera vuelve a salir la}\\&\text{integral original, entonces podemos escribir}\\&\\&I = (ln\,x)^3 - 2 I\\&\\&3I = (ln\,x)^3\\&\\&I=\frac{(ln\,x)^3}{3}+C\end{align}$$Que como puedes ver es el mismo resultado que el obtenido por sustitución y que era el que yo habría usado con probabilidad 100% de no decir que se tenía que resolver por partes.
·
Y eso es todo.
No has debido fijarte y has votado buena en lugar de excelente. Puedes cambiar la puntuación y no ha pasado nada.