Me explican este ejercicio de integrales

·

Supongo que tendrás los graficos de esto. Tomas la función oferta y demanda. La demanda es decreciente y la oferta creciente has que se cortan. Entonces trazas una segemento horizontal hacia la izquierda desde el punto de eqilibrio hasta el eje Y.

La zona de arriba que está entre ese segmento horizontal y la función de la demanda es el excedente del consumidosr. Y la parte de abajo que está entre la función de la demanda y ese segmento es el excedente del productor.

El escedente del consumidor es el dinero que se han ahorrado los consumidores que estaban dispuestos a pagar un precio mayor al de equilibrio. Y el excedente del productor es el dinero que ha ganado el productor por vender al precio de equilibrio en lugar de a otros más bajos.

Si las funciones son lineales estas regiones son triángulos y se puede calcular su área fácilmente. Pero si son funciones más complicadas se deben calcular mediante integrales

Si S(x) es la función de oferta, D(x) la de la demanda y (qo, po) el precio de equilibrio tenemos

$$\begin{align}&E_c=\int_0^{q_0}(D(x)-p_0)dx=\\&\\&\left.\int_0^{q_0}D(x)dx - p_0x\right|_0^{q_0}=\\&\\&\int_0^{q_0}D(x)dx-p_0q_0\\&\\&\\&\\&E_p=\int_0^{q_0}(p_0-S(x))dx=\\&\\&p_0x \bigg {|}_0^{q_0}-\int_0^{q_0}S(x)dx =\\&\\&p_0q_0-\int_0^{q_0}S(x)dx\end{align}$$

Lo primero que debe hacerse es calcular el punto de equilibrio

x= - x/3 + 4

4x/3=4

x/3=1

x=3  ==> q0 = 3

S(x) = x = 3  ==> p0 = 3

$$\begin{align}&E_c=\int_0^3\left(-\frac x3+4\right)dx-3·3=\\&\\&\left[-\frac{x^2}{6}+4x  \right]_0^{3}-9=-\frac 96+12-9=\\&\\&-\frac 32+3= \frac 32=1.5\\&\\&\\&E_p=3·3 -\int_0^{3} x\;dx=\\&\\&9-\left.\frac {x^2}2\right|_0^3=9 -\frac 92=\frac 92=4.5\end{align}$$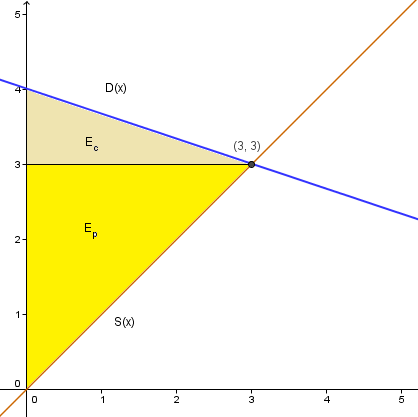

Y eso es todo.