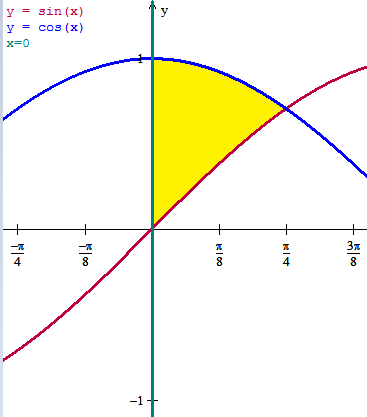
Determinar el volumen que se obtiene al hacer girar sobre el eje X, en el primer cuadrante, las curvas dadas por las ecuaciones
Me pueden ayudar a determinar el volumen que se obtiene al hacer girar sobre el eje X, en el primer cuadrante, las curvas dadas por las ecuaciones: y=senx, y=cosx, x=0
1 respuesta
Respuesta de Valero Angel Serrano Mercadal
2