Cómo determinar el volumen de de un sólido en cálculo integral?
Determinar el volumen del sólido generado al hacer girar con respecto a la recta x=3, la región comprendida entre la parábola x=y^2 y la recta x=3
1 Respuesta
·
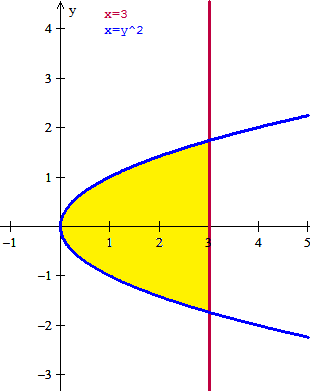
Trasladaremos la recta x=3 a la recta x=0, de esta forma el problema es el de girar una curva alrededor del eje Y que es algo que sabemos hacer. Esta traslación consiste en restar 3 a las coordenada x, por ello queda que la recta x=3 se queda en x=0, y la parábola x=y^2 quedará en
x = y^2 - 3
Los puntos de intersección de esta nueva parábola con el eje Y son
0 = y^2 -3
y= +- sqrt(3)
Y aplicando la fórmula del volumen
$$\begin{align}&V=\pi\int_{y_1}^{y_2} [f(y)]^2dy\\&\\&V =\pi\int_{-\sqrt 3}^{\sqrt 3}(y^2-3)^2dy=\\&\\&\pi \int_{-\sqrt 3}^{\sqrt 3}(y^4-6y^2+9)dy=\\&\\&\pi\left[\frac{y^5}{5}-2y^3+9y \right]_{-\sqrt 3}^\sqrt 3=\\&\\&\pi\left(\frac{9 \sqrt 3}{5}-2·3 \sqrt 3+9 \sqrt 3+\frac{9 \sqrt 3}{5}-2·3 \sqrt 3+9 \sqrt 3 \right)=\\&\\&\pi\left(\frac{18 \sqrt 3}{5}-12 \sqrt 3+18 \sqrt 3 \right)=\pi\left(\frac{18 \sqrt 3}{5}+6 \sqrt 3 \right)=\\&\\&\frac{48 \sqrt 3\; \pi}{5}\approx52.23742169\\&\\&\end{align}$$·
Y eso es todo.
Me puede apoyar a realizar la gráfica por favor para ver cómo queda. Saludos
Si claro. Lo que pasa es que yo pienso que es mejor si puedes hacer este tipo de ejercicios sin necesidad de hacer los gráficos, pero claro yo he hecho muchos y me parecen fáciles.
Como puedes ver si pones al poner la recta y=3 como eje de giro la ecuación de la parabola se transforma en x=y^2 -3
Y eso es todo.
