Máximos, mínimos o puntos de inflexión
Hallar, si existen, máximos, mínimos, puntos de inflexión o asíntotas de las siguientes funciones:
$$\begin{align}&f) f(x)=(x-1)^3(x-3)\\&\\&b) f(x)= \frac{x^2}{\sqrt{4+x^2}}\\&\\&h)f(x)=x^2-\frac{2}{x}\\&\end{align}$$
1 Respuesta
Respuesta de Lucas m
1
Maar Hammet!
Has de enviar un ejercicio por pregunta.
Te haré la primera
f) Es una función polinómica: no tiene asíntotas
Los máximos y mínimos se calculan igualando la derivada primera a cero
Los puntos de inflexión se calculan igualando la derivada segunda a cero
$$\begin{align}&y=(x-1)^3(x-3)\\&\\&y'=3(x-1)^2(x-3)+(x-1)^3·1=\\&factor \ común\\&= (x-1)^2 \Bigg [3(x-3)+(x-1) \Bigg]=\\&\\&=(x-1)^2[4x-10]\\&y'=0\\&\Rightarrow\\&x=1\\&x=\frac{10}{4}=\frac{5}{2}\\&\\&Criterio \ de \ la \ segunda \ derivada:\\&\\&y''(x)=2(x-1)[4x-10]+(x-1)^2·4=factor \ común=\\&\\&=(x-1) \Bigg[2(4x-10)+(x-1)·4 \Bigg]=\\&=(x-1)[12x-24]\\&\\&y''(1)=0 \ no \ decide\\&y''(\frac{5}{2})=(\frac{5}{2}-1)[8·\frac{5}{2}-24]>0 \Rightarrow mínimo\\&f(\frac{5}{2})=(\frac{5}{2}-1)^3(\frac{5}{2}-3)=\frac{-27}{16}\\&\\&Puntos \ inflexión\\&y"=0 \Rightarrow (x-1)[12x-24]=0\\&x=1\\&x=\frac{24}{12}=2\\&Criterio \ derivada \ tercera\\&y'''=1(12x-24)+(x-1)12=24x-36\\&y'''(1) \neq0\\&y''' (2)\neq0\\&Puntos \ inflexión:\\&(1,0)\\&(2,-1)\end{align}$$La comprobación de los máximos y mínimos también se puede hacer estudiando los intervalos de crecimiento (Criterio de la derivada primera)
La comprobación de los puntos de inflexión también se puede hacer estudiando los intervalos de Concavidad (criterio de la derivada segunda)
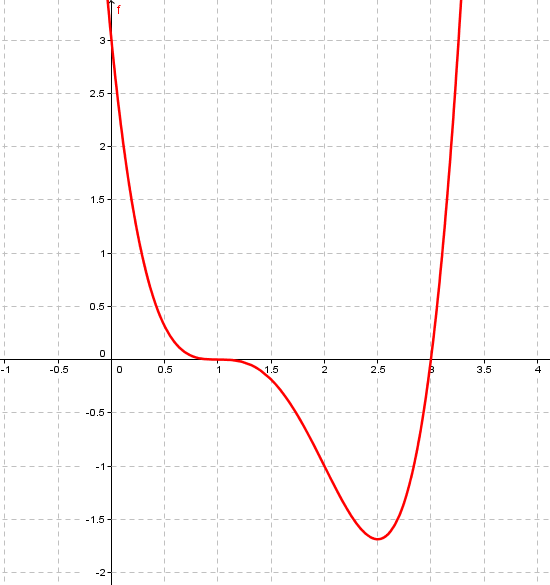
Graficando:
