Hallar máximos, mínimos, puntos de inflexión o asíntotas

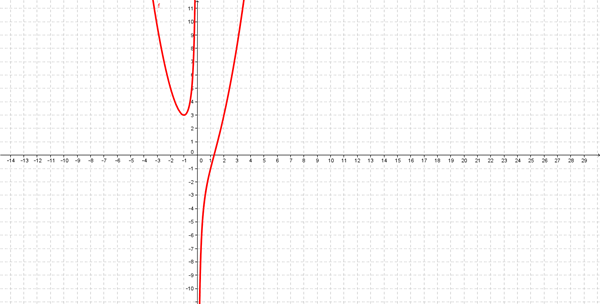
$$\begin{align}&y=x^2-\frac{2}{x}=\frac{x^3-2}{x}\\&\\&Domf= \ R-\{0\}\\&\lim_{x \to 0}f(x)= \infty\\&x=0 \ Asintota \ Vertical\\&\\&y'=\frac{3x^2·x-1(x^3-2)}{x^2}=\frac{2x^3+2}{x^2}\\&\\&y'=0\\&2x^3+2=0\\&x=\sqrt [3]{-1}=-1\\&\\&y''=\frac{6x^2·x^2-2x(2x^3+2)}{x^4}=\frac{2x^4-4x}{x^4}=\frac{2x^3-4}{x^3}\\&\\&y''(-1)=\frac{-6}{-1}>0 \Rightarrow mínimo \ en (-1,3)\\&\\&f(-1)=\frac{(-1)^3-2}{-1}=3\\&\\&Puntos \ Inflexión:\\&\\&y''=0 \Rightarrow \frac{2x^3-4}{x^3}=0\\&\\&2x^3=4\\&\\&x=\sqrt[3]{2}=1.259992105\\&Criterio \ derivada \ segunda\\&f''(x^-)=f''(1)=\frac{2-4}{1}<0 \ convexa(hacia \  abajo)\\&f''(x^+)=f''(2)=\frac{2·2^3-4}{2^3}>0\Rightarrow cóncova( \ hacia \ arriba)\\&Punt Inflexión\\&f(\sqrt[3]{2})=\frac{\sqrt[3]{2}^3-2}{\sqrt[3]{2}}=0\\&P.I.(\sqrt[3]{2},0)\end{align}$$

Hola Maar Hammet!!

Graficando: