Determine centro, radio y grafique circunferencia

·

La ecuación canónica de una circunferencia es

(x-h)^2 + (y-k)^2 = R^2

Donde (h, k) es el centro y R el radio.

Debes dejar la ecuación de esa forma y la técnica a usar se llama completar cuadrados consiste en que

x^2+ 2ax = (x+a)^2 - a^2

Entonces debes tomar los elementos como el término de la izquierda que tengas en la ecuacion y sustituirlos por el término derecho. El valor de a se obtiene dividiendo por 2 el coeficiente del término de la x. Lo que he dicho para x también se hace con la y.

Lo malo de este ejercicio es que no tenemos x^2 sino 9x^2 y ya he visto que no se puede dividir todo por 9, luego nos tocará lidiar con números fraccionarios, no se te ocurra usar los decimales hacen feísimo. Asi que lo primero dividimos todo por 9 y queda

$$\begin{align}&x^2 + y^2 + \frac 43x - \frac 23y + \frac 49 = 0\\&\\&\text{Hago los cambios aparte para que los veas }\\&\text{pero en la práctica se hace todo seguido} \\&x^2+\frac 43x=\left(x+\frac 23  \right)^2-\frac 49\\&\\&y^2-\frac 23y=\left(y-\frac 13  \right)^2-\frac 19\\&\\&\text{Y sustituyendo e la ecuación tenemos}\\&\\&\left(x+\frac 23  \right)^2-\frac 49 +\left(y-\frac 13  \right)^2-\frac {1}{9}+\frac 49=0\\&\\&\left(x+\frac 23  \right)^2 +\left(y-\frac 13  \right)^2=\frac{1}{9}\\&\\&\left(x+\frac 23  \right)^2 +\left(y-\frac 13  \right)^2=\left(\frac 13  \right)^2\\&\\&\\&\text{Luego es centro es }\left(-\frac 23,\;\frac 13  \right) \\&\\&\text{y el radio es: }\quad R=\frac{1}{3}\end{align}$$

Y esta es la gráfica:

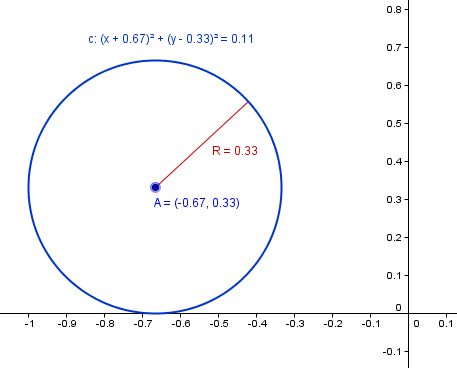
Y eso es todo.