Como determinar ecuación general y graficar

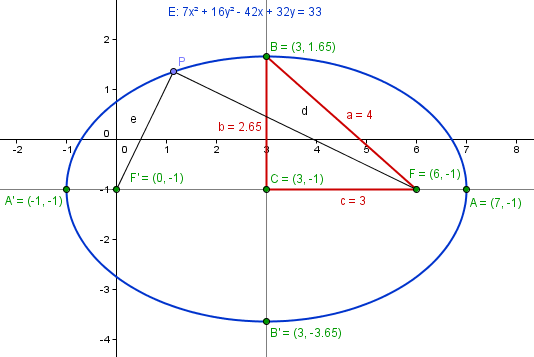
El semieje paralelo al eje X es la distancia del centro a los vértices de ese eje. Tal como nos lo ponen no hay siquiera que calcular, es 4.

Ahora habría que calcular el semieje paralelo al eje Y.

Para ello nos dan la semidistancia focal c, que es la distancia del centro a los focos, que es 3.

Y la relación que hay entre estas distancias es

(semieje mayor)^2 - (semieje menor)^2 = (distancia focal)^2

que en los libros lo ponen como

a^2 - b^2 = c^2

Pero si lo usas así debes tener cuidado, la letra a no es siempre la del eje X, si el semieje paralelo al eje Y es mayor el que debe llevar la letra a es este.

En este ejercicio nos dicen que los focos están en el eje paralelo al eje X, luego el semieje mayor es este y ya podemos asegurar que a=4

Luego la igualdad es

4^2 - b^2 = 3^2

16 -b^2 = 9

b = sqrt(16-9)

b=sqrt(7)

Y la ecuación canónica de una elipse es:

$$\begin{align}&\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\\&\\&\text{donde (h,k) es el centro}\\&\\&\text{luego la ecuación canónica de esta elipse es}\\&\\&\frac{(x-3)^2}{4^2}+\frac{(y+1)^2}{(\sqrt 7)^2}=1\\&\\&\frac{x^2-6x+9}{16}+\frac{y^2+2y+1}{7}=1\\&\\&\text{multiplicamos por }16·7=112\\&\\&7x^2-42x+63+16y^2+32y+16=112\\&\\&7x^2+16y^2-42x+32y-33=0\end{align}$$

Y esta es la gráfica.

Y eso es todo.