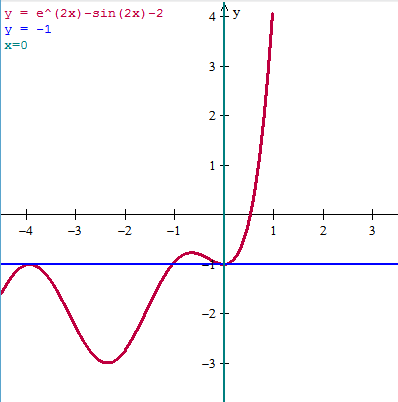
Hallar ecuaciones de la recta tangente y recta normal.
Hallar las ecuaciones de la recta tangente y de la recta normal en los puntos indicados:
$$\begin{align}&g)\ e^{2x}-sen(2x)-2\ \ \ en \ \ \ x_{0}=0\end{align}$$Al intentar hacerlo me ha dado una constante para la recta tangente y lo mismo para la recta normal pero tengo mis dudas de haberlo hecho correctamente.
2 Respuestas
Respuesta
2
En principio es correcto tu resultado. Veamos por qué:
$$\begin{align}&g(x) = e^{2x} - sen(2x) - 2\\&g'(x) = 2e^{2x}-2cos(2x)\\&g'(x) = 2e^{2(0)}-2cos(2(0))=2-2=0\end{align}$$Como ves la derivada en x=0 da cero, esto significa que la recta tangente es horizontal, y la recta que es normal a una horizontal, sin dudas será vertical.
Respuesta de Valero Angel Serrano Mercadal
2
·
$$\begin{align}&f(x) = e^{2x}-sen(2x)-2\\&\\&f'(x) = 2e^x-2cosx\\&\\&f'(0) = 2e^0 - 2cos0 = 2·1-2·1 = 0\\&\\&\text{La recta tangente es}\\&\\&y=y_0+0(x-x_0)\\&\\&y=y_0\\&\\&Como \\&\\&y_0=f(0) = e^0-sen0-2=1-0-2=-1\\&\\&y=-1\\&\\&\text{Y la normal es vertical que pasa por x=0, luego es}\\&\\&x=0\end{align}$$Y esta es la gráfica.
Y eso es todo.