Tengo una duda con este ejercicio de Hipérbole - MATEMÁTICA

Alex Mate!

·

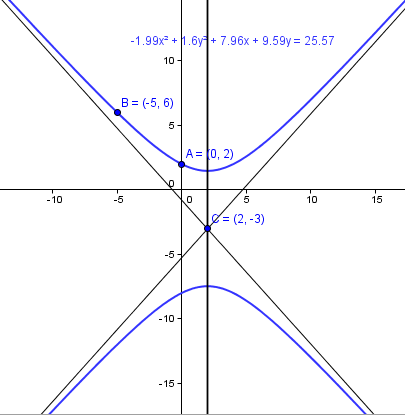
Por ser el eje focal paralelo al eje Y la y es la variable que lleva el signo - y el divisor a^2

$$\begin{align}&\frac{(y+3)^2}{a^2}-\frac{(x-2)^2}{b^2}= 1\\&\\&\text{Por pasar por el punto(0,2)}\\&\frac {25}{a^2}-\frac 4{b^2}=1\implies25b^2-4a^2=a^2b^2\implies\\&\\&b^2=\frac {4a^2}{25-a^2}\\&\\&\text{Por pasar por(-5,6)}\\&\frac{81}{a^2}-\frac{49}{b^2}=1\implies 81b^2-49a^2=a^2b^2 \implies\\&\\&b^2= \frac{49a^2}{81-a^2}\\&\\&\frac {4a^2}{25-a^2}=\frac{49a^2}{81-a^2}\\&\\&4(81-a^2) =49(25-a^2)\\&\\&324-4a^2=1225-49a^2\\&\\&45a^2 = 901\\&\\&a^2=\frac{901}{45}\\&\\&b^2=\frac{4·\frac{901}{45}}{25-\frac{901}{45}}=\frac{901}{56}\end{align}$$

Y una vez calculados a^2 y b^2 los sustituyes en la ecuación canónica y dejas esa ecuación o la pones en forma general o la dejas como quieras.

Y eso es todo.