Tengo una duda con este ejercicio de Hipérbola en matemática

$$\begin{align}& \end{align}$$

¡Hola Alex!

·

La asíntotas se cortan en el centro (0, -1)

Y el foco es ta en el punto (-3sqrt(3), -1)

Luego centro y foco están en la horizontal y=-1, eso significa que la variable x es la que lleva el signo positivo, por lo tanto la ecuación será:

$$\begin{align}&\frac{x^2}{a^2}-\frac{(y+1)^2}{b^2}=1\\&\\&\text{La pendiente de la asíntota será}\\&m=\frac{5-(-1)}{4-0}=\frac 64=\frac 32\\&\\&\text{Es positiva, corresponde a }\frac ba\\&\\&\frac ba = \frac 32\implies b=\frac {3a}2\\&\\&\text{Y la semidistancia focal es}\\&\\&c=3 \sqrt 3=\sqrt {a^2+b^2}\\&\\&\text{susituimos b por lo calculado antes}\\&\\&\sqrt{a^2+\frac{9a^2}{4}}=3 \sqrt 3\\&\\&\frac{13a^2}{4}=27\\&\\&a^2=\frac{108}{13}\\&\\&b^2= \frac{9a^2}4=\frac{243}{13}\\&\\&\text{Luego la ecuación canónica es}\\&\\&\frac{x^2}{\left(\sqrt \frac{108}{13}  \right)^2}-\frac{(y+1)^2}{\left(\sqrt \frac{243}{13}  \right)^2}=1\end{align}$$

Y esta es la gráfica

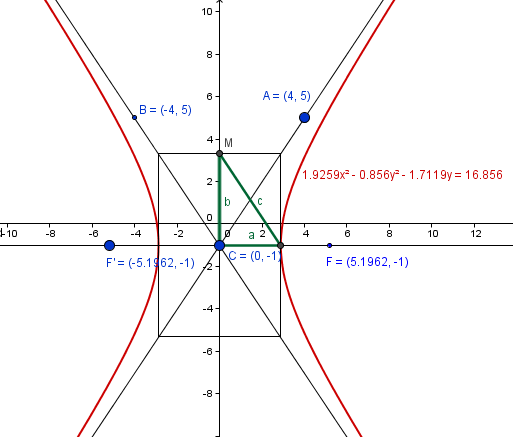
Y eso es todo.