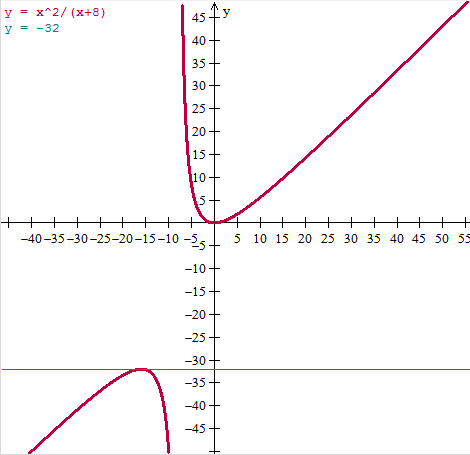Calcula el dominio y el rango de la Siguiente relacion:

·

Las funciones x^2, x+8, son polinomios que están definidos en todo R. Unicamente dejera de estar definida la función cociente en aquellos puntos donde el denominador sea 0

x+8 = 0

x = -8

Luego

Dom f = R - {-8}

Y el rango es el dominio de la función inversa, la calculamos despejando la x en la función:

$$\begin{align}&y = \frac{x^2}{x+8}\\&\\&xy+8y = x^2\\&\\&x^2-xy-8y =0 \\&\\&\text{esto es una ecuación de segundo grado}\\&\\&x=\frac{y\pm \sqrt{y^2+32y}}{2}\\&\\&\text{la ponemos con x como variable independiente}\\&\\&f^{-1}(x) = \frac{x\pm \sqrt{x^2+32x}}{2}\\&\\&\text{Para que este definida debe ser}\\&x^2+32x\ge0\\&x(x+32)\ge 0\\&\\&Si\; x\ge 0\implies x+32\ge 0\implies x(x+32)\ge0\\&Si\;x\le-32\implies x+32\le0\implies x(x+32)\ge 0\\&\\&Luego\\&\\&Rango\; f=Dom \;f^{-1}=(-\infty,-32]\cup[0,\infty)\end{align}$$

Y que mejor que hacer la fráfica para confirmarlo

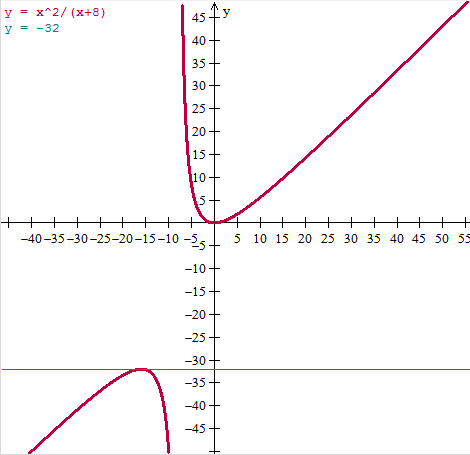
Y eso es todo.