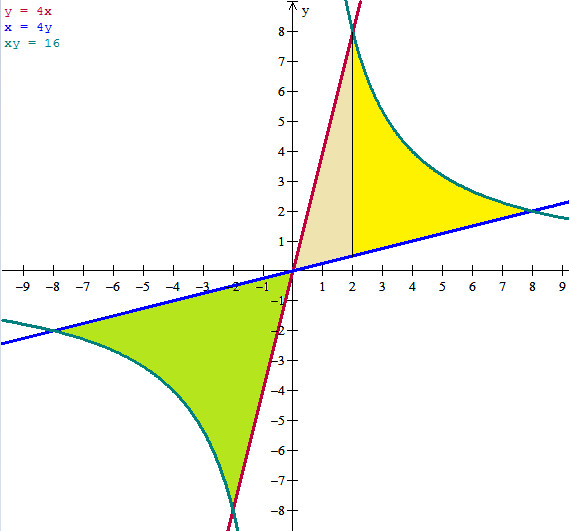Calcular el volumen del sólido generado al rotar R en torno al eje X

·

Recuerda que ya conteste la parte del área en esta pregunta

http://www.todoexpertos.com/preguntas/63sq4gbstpq4w9pa/calcular-area-y-volumen-de-solidos-en-revolucion?selectedanswerid=63t3s3xdetxlgqxu

Discrepamos con Lucas porque como no dice nada de que deba ser en el primer cuadrante yo tomo también el área definida en el tercer cuadrante y el área es el doble. Por eso mismo yo también te voy a dar el doble de volumen si coincidimos en el resto de las cuentas.

Te adjunto la misma imagen que usé entonces y las intersecciones ya las doy por calculadas que eran tontas pero las calculé.

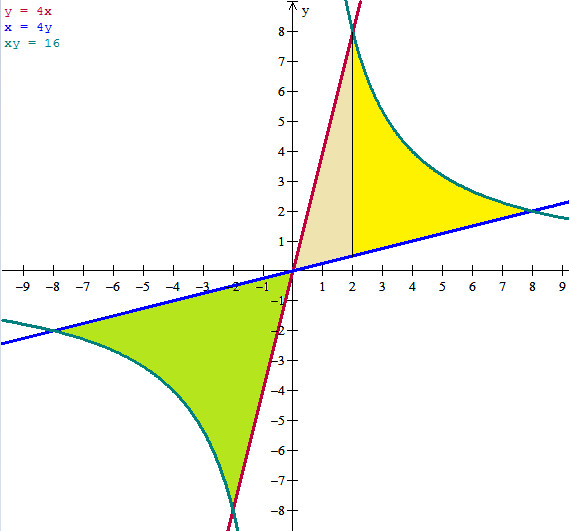
Calcularemos el volumen engendrado en la parte derecha y lo multiplicaremos por dos.  De nuevo hay que tomar dos trozos ya que la función superior cambia, ya habíamos calculado que los límites eran [0, 2]  y [2, 8]

$$\begin{align}&V=\pi\int_{x_1}^{x_2}\left(f(x)^2-g(x)^2\right)dx\\&\\&V=\pi\int_0^2\left((4x)^2-\left(\frac{x}{4}\right)^2  \right)dx+\\&\\&\qquad\pi\int_2^8\left( \left(\frac{16}{x}  \right)^2 -\left(\frac{x}{4}\right)^2\right)=\\&\\&\\&\pi \int_0^2\left( 16x^2-\frac{x^2}{16} \right)dx+\pi\int_2^8 \left(\frac{256}{x^2}-\frac{x^2}{16}\right)dx=\\&\\&\pi \left(\frac{255}{16}\int_0^2 x^2 dx-256 \frac 1x\bigg|_2^8-\frac{1}{48}x^3\bigg|_2^8 \right)=\\&\\&\pi \left( \frac{255}{48}x^3\bigg|_0^2  -32+128-\frac{512}{48}+\frac 8{48}\right)=\\&\\&\pi\left(\frac {255}6+96 -\frac{504}{48}  \right)=\\&\\&\pi \left(\frac{255}{6}+\frac{576}{6}-\frac{63}{6}  \right)=128\pi\\&\\&\text{Y en la izquierda el mismo volumen por simetría luego}\\&\\&V_T=256\pi\end{align}$$

Y eso es todo.

Son dos problemas en uno, tendrías que mandarlo en dos preguntas:

Los puntos de corte se calculan resolviendo dos sistemas:

$$\begin{align}&y=4x\\&y=\frac{16}{x}\\&\\&4x=\frac{16}{x}\\&x^2=4\\&x=2\\&\\&\\&y=\frac{x}{4}\\&y=\frac{16}{x}\\&\frac{x}{4}=\frac{16}{x}\\&x^2=64\\&x=8\\&\\&Area=\int_0^2(4x-\frac{1}{4}x)dx+\int_2^8(\frac{16}{x}-\frac{1}{4}x)dx=\\&\\&\int_0^2 \frac{15}{4}xdx+\int_2^8(\frac{16}{x}-\frac{1}{4}x)dx=\\&\\&\frac{15}{4} \Bigg[\frac{x^2}{2}\Bigg]_0^2+\Bigg[16lnx-\frac{x^2}{8} \Bigg]_2^8=\\&\\&\frac{15}{2}+16ln8-8-(16ln2-\frac{4}{8})=\\&16ln2^3-16ln2=48ln2-16ln2=32ln2 \simeq22,18 \ u^2\\&\\&\\&V=\pi \int_a^b(y_2^2-y_1^2)dx\\&\\&V_1=\pi \int_0^2(4x)^2-(\frac{1}{4}x)^2  \ dx=\\&\\&\pi \int_0^216x^2-\frac{x^2}{16})dx=\pi \int_0^2 \frac{255}{16}x^2dx=\\&\\&\pi \frac{255}{16} \Bigg [\frac{x^3}{3} \Bigg]_0^2=\frac{85}{2}\pi\\&\\&V_2=\pi \int_2^8(\frac{16}{x})^2-(\frac{1}{4}x)^2 \ dx=\\&\\&\pi \int_2^8 \frac{256}{x^2}-\frac{1}{16}x^2)dx=\\&\\&\pi 256 \Bigg [\frac{x^{-1}}{-1} \Bigg ]_2^8- \pi \frac{1}{16} \Bigg [ \frac{x^3}{3} \Bigg ]_2^8=\\&\\&256 \pi (-\frac{1}{8}+\frac{1}{2})-\pi \frac{1}{48}(8^3-2^3)=\\&\\&:::::::::::::::::::::=128 \pi \ u^3\simeq 402,12 \ u^3\end{align}$$