Analiza dominio, rango y gráfica de las siguientes funciones:

Te haré la c y d

$$\begin{align}&c)\\&f(x)=\frac{x^2+x}{x}\\&Dom= \mathbb{R}- \{0 \}\\&y=\frac{x(x+1)}{x}=x+1\\&\\&\\&\\&\\&d)\\&\\&\\&f(x)=\frac{x^2-1}{x+1}\\&\\&x+1=0\\&x=-1\\&Domf(x)=\mathbb{R}- \{-1 \}\\&\\&y=\frac{(x+1)(x-1)}{x+1}=x-1\end{align}$$

c) La gráfica c es igual a la recta y=x+1 , excepto en x=0 donde no está definida

Rango=R-{1}

d) La gráfica es igual a la recta y=x-1, excepto en el punto x=1, donde hay una discontinuidad evitable(un hueco), ya que allí f(x) no está definida

Rango=R-{-2}

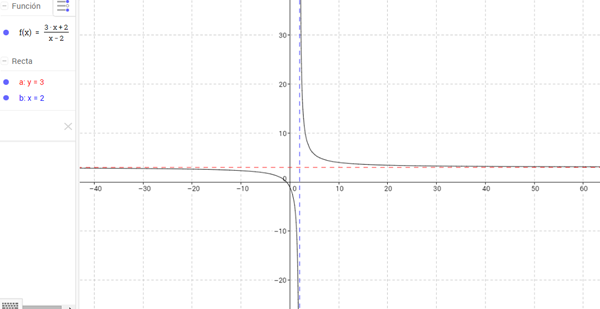
$$\begin{align}& \end{align}$$

Vamos entonces por la a) a ver que sale

$$\begin{align}&a) f(x)=\frac{3x+2}{x-2} \mbox{ (supongo que es así, sino avisa ya que no tiene sentido 3+2)}\\&\mbox{Dom: todos los puntos donde está definida la función, los polinomios están definidos para todo R}\\&\mbox{así que solo queda ver los puntos donde se anula el denominador que sería cuando x-2=0, o sea}\\&\mbox{cuando x=2}\\&\mbox{Rango: para esto tenemos que ver los posibles valores de la función}\\&\mbox{ya sabemos que para x=2 no está definida, y tiene una asintota vertical, haciendo abuso de notación}\\&\lim_{x \to 2^+}\frac{3x+2}{x-2} \to \frac{8}{0^+}\to +\infty\\&\lim_{x \to 2^-}\frac{3x+2}{x-2} \to \frac{8}{0^-}\to -\infty\\&\mbox{Ahora veamos los límites cuando x tiende a infinito}\\&\lim_{x \to +\infty}\frac{3x+2}{x-2} \to \frac{3(+\infty)}{+\infty} \to +3\\&\lim_{x \to -\infty}\frac{3x+2}{x-2}  \to \frac{3(-\infty)}{-\infty} \to +3\\&\mbox{Veamos si f(x) = 3 para algún valor de x}\\&3=\frac{3x+2}{x-2}\\&3(x-2)=3x+2\\&3x-6=3x+2\\&-6=2 \mbox{      Absurdo!, luego 3 no pertenece al Rango de f(x)}\\&\mbox{Análicemos la derivada}\\&a) f'(x)=\frac{3}{(x-2)} -\frac{(3x+2)}{(x-2)^{2}}=\frac{3(x-2)-(3x+2)}{(x-2)^{2}}=\frac{3x-6-3x-2}{(x-2)^{2}}=\frac{-8}{(x-2)^{2}}\\&\mbox{Para el Dom f está siempre definida y es siempre menor que cero, así que la función es estricatamente}\\&\mbox{decreciente}\\&\mbox{De todo lo anterior podemos concluir que el rango es R -{3}}\\&\end{align}$$

Inicialmente iba a hacer también la b) pero, como ves, llevó demasiado trabajo. Te dejo además la imagen de la función anterior donde te marco las dos asíntotas que tiene