Como hallar las asintotas oblicuas en:

·

Recuerda que hay que mandar un ejercicio por pregunta. Hago el primero y si quieres el segndo mándalo en otra pregunta.

La asíntota será

y=mx+b

La pendiente de asíntota oblicua es el limite en infinito de la función entre x.

Ojo, puede haber una asíntota oblicua en - infinito y otra en infinito que sean distintas.

$$\begin{align}&m=\lim_{x\to \infty}\frac{\frac{x^3}{2(x+1)^2}}{x}= \lim_{x\to\infty}\frac{x^2}{2(x+1)^2}=\\&\\&\lim_{x\to\infty} \frac{x^2}{2x^2+4x+2}=\\&\\&\text{dividimos todo por }x^2\\&\\&\lim_{x\to\infty} \frac{1}{2+\frac{4}{x}+\frac{2}{x^2}}=\frac 12\end{align}$$

Y elemento b se calcula como el límite en infinito de f(x) - mx

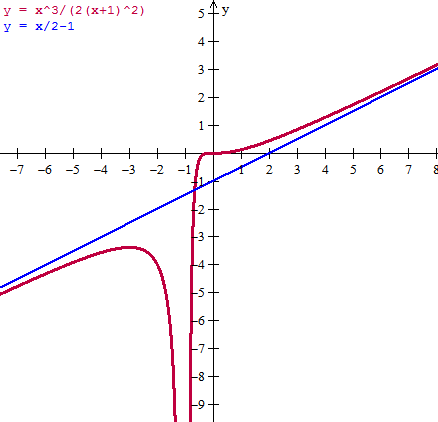
$$\begin{align}&b=\lim_{x\to\infty}\left(\frac{x^3}{2(x+1)^2}-\frac x2\right) =\\&\\&\lim_{x\to\infty}\frac{x^3-x(x+1)^2}{2(x+1)^2}=\\&\\&\lim_{x\to\infty}\frac{x^3-x^3-2x^2-x}{2(x+1)^2}=\\&\\&\lim_{x\to\infty}\frac{-2x^2-x}{2x^2+4x+2}=\\&\\&\text{Y dividiendo todo entre }x^2\\&\\&\lim_{x\to\infty}\frac{-2-\frac 1x}{2+\frac 4x+\frac 2{x^2}}=\frac{-2}{2}=-1\\&\\&\text{Luego la asíntota oblicua es}\\&\\&y=\frac x2-1\end{align}$$

Lo comprobaremos con la gráfica

Te hago la otra (confirma que el enunciado es de la forma que lo interpreté)

$$\begin{align}&y= \frac{x^3}{x^2-1}\\&\mbox{La asíntota es de la forma y=mx+b}\\&Veamos\\&m= \lim_{x \to \infty} \frac{\frac{x^3}{x^2-1}}{x}=\lim_{x \to \infty} \frac{x^2}{x^2-1}\\&\mbox{Dividiendo por x cuadrado el denominador}\\&\lim_{x \to \infty} \frac{x^2}{x^2(1- \frac{1}{x^2})}=\lim_{x \to \infty} \frac{1}{1(1- \frac{1}{x^2})} \to 1\\&\mbox{Así que la asíntota será de la forma y=x+b, calculemos b}\\&b= \lim_{x \to \infty} \frac{x^3}{x^2-1}-{x}=\lim_{x \to \infty} \frac{x^3-x(x^2-1)}{x^2-1}=\\&\lim_{x \to \infty} \frac{x^3-x^3+x}{x^2-1}=\lim_{x \to \infty} \frac{x}{x^2-1} \\&\mbox{Dividiendo por x el denominador}\\&\lim_{x \to \infty} \frac{x}{x(x-1)} =\lim_{x \to \infty} \frac{1}{(x-1)} \to 0\\&{así que la recta asíntota es y=x, veamos la gráfica}\\&\end{align}$$