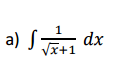
2 Respuestas
Respuesta de Valero Angel Serrano Mercadal
1
$$\begin{align}&\int \frac{1}{1+\sqrt x}dx=\\&\\&t=1+\sqrt x\implies \sqrt x=t-1\\&dt=\frac{dx}{2 \sqrt x}\implies dx=2 \sqrt xdt=2(t-1)dt\\&\\&=\int \frac 1t·2(t-1)dt=\\&\\&2\int\left(1-\frac 1t\right)dt= \\&\\&2t-2 ln|t|+C=\\&\\&2(1+\sqrt x)-2 ln|1+\sqrt x|+C=\\&\\&2(1+\sqrt x) - 2ln(1+\sqrt x)+C\end{align}$$·
Y eso es todo.
La integral está bien así, pero se puede echar la constante 2 al contenedor de las constantes y queda más simplificada.
$$\begin{align}&2\sqrt x - 2ln(1+\sqrt x)+C\end{align}$$
Respuesta de Lucas m
1
$$\begin{align}&x=t^2 \Rightarrow dx=2tdt\\&\\&\int \frac{1}{1+\sqrt x}dx=\int \frac{1}{1+t} 2tdt=\\&\\&=\int \frac{2t}{t+1}dt= \int (2 +\frac{-2}{t+1})dt=\\&\\&=2t-2ln|t+1|=2 \sqrt x-2 ln|\sqrt x+1|+C\end{align}$$donde 2t/(t+1) da 2 de cociente y -2 de resto por lo que:
$$\begin{align}&\frac{2t}{t+1}=2-\frac{2}{t+1}\end{align}$$