Problema de probabilidad: un dado...
Un dado de 6 caras se lanza hasta que el total sea mayor a 400, o sea, que se suman los resultados hasta que la adición sea mayor a 400. ¿Cuál es la probabilidad de que se necesita más de 140 tiros? Se puede utilizar una aproximación.
1 Respuesta
·
Por el teorema central del límite (o del límite central):
Sea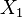 
, 
, ..., 
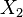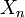un conjunto de variables aleatorias, independientes e idénticamente distribuidas de una distribución con media μ y varianza σ^2≠0. Entonces, si n es suficientemente grande, la variable aleatoria
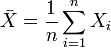
tiene aproximadamente una distribución normal con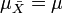 
y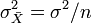 
.
·
n=140 se considera suficientemente grande, entonces la variable aleatoria media de los 140 tiros es aproximadamente una normal con:
$$\begin{align}&\mu_{\overline X} = \mu=\frac{1+2+3+4+5+6}{6} = \frac{21}6 = 3.5\\&\\&\sigma^2_{\overline X}=\frac{\sigma^2}n=\frac{\frac{\sum_{i=1}^6 i^2}{6}-\mu_{\overline X}^2}{n}=\\&\\&\frac{\frac{1+4+9+16+25+36}{6}-3.5^2}{140}=\frac 1{48}=0.0208333333...\\&\\&\sigma_{\overline X}= \sqrt{\sigma^2_{\overline X}}=\frac{1}{4 \sqrt 3} =\frac{\sqrt 3}{12}\approx 0.1443375673\\&\\&\overline X\to N(3.5,\;0.1443375673)\\&\\&\text{Para que puntos}\le 400 \text{ el promedio debe ser}\\&\\&prom\le \frac{400}{140}= \frac{20}{7}= 2.857142857\\&\\&P(\overline X\le 2.8571428) = P\left(Z\le \frac{2.8571428-3.5}{0.1443375673} \right)=\\&\\&P(Z \le -4.453844934)= 1-P(Z\le 4.453844934)=\\&\\&\text{las tablas normales no llegan a tanto}\\&\\&1-0.9999957807914 =0.0000042192086\\&\end{align}$$La probabilidad es prácticamente nula, se ha debido tener 401 p más de suma con los 140 lanzamientos.
Y eso es todo.
