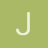Pasos para derivadas en calculo
Realizar las siguientes derivadas
a) y=5x3+8x2+2x+x
b) y=arc cot 1+x/ 1-x2
c) y= x2 arc cos x
Nota la "x" de la función coseno es coeficiente
Respuesta de Valero Angel Serrano Mercadal
1
la primera es correcta
la segunda la b) es arc cot en vez de arctg
la tercera c) es arc cos x en vez de arcos
La notación no es tan uniforme como puedas pensar, yo toda la vida he usado arcos para arccos no por me diera la gana sino porque me enseñaron así. Y del arco cotangente es una función tan rara que no recuerdo como se escribiría, pero en consonancia con
tangente = tg
cotangente = ctg
La escribiría arcctg
Bueno vamos con las derivadas
$$\begin{align}&a)\quad y=5x^3+8x^2+2x+x=5x^3+8x^2+3x\\&\qquad y'=15x^2+16x+3\\&\\&\\&\\&b)\quad y= arc\; cot \left(\frac{1+x}{1-x^2} \right)=\\&\text{en esta viene muy bien simplificar antes.}\\&\text{Como }1-x^2=(1+x)(1-x)\\&\\&=arc\;cot\left(\frac 1{1-x}\right)\\&\\&y'= -\frac{1}{1+\left(\frac{1}{1-x} \right)^2}·\frac{-1}{(1-x)^2}·(-1)=\\&\\&-\frac{1}{\frac{(1-x)^2+1}{(1-x)^2}}·\frac{1}{(1-x)^2}=-\frac{1}{(1-x)^2+1}=\\&\\&-\frac{1}{x^2-2x+2}\\&\\&\\&\\&\\&c)\quad y=x^2\,arcos\,x\\&\\&y'=2x·arcos\,x+x^2·\frac{-1}{\sqrt{1-x^2}}=\\&\\&\qquad 2x·arcos\,x-\frac{x^2}{\sqrt{1-x^2}}\end{align}$$
