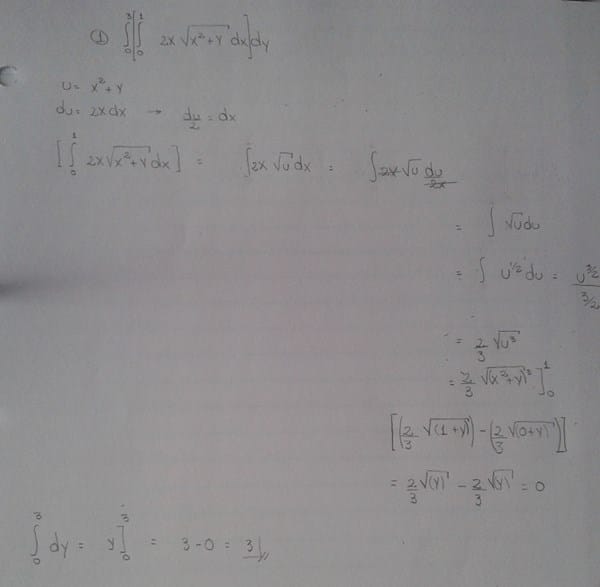¿Desearía me asesore en este ejercicio, y si mantengo error me lo haga saber, integrales dobles mediante cambio de variable?

$$\begin{align}&\text{Resolveré el ejercicio, para que compares y despejes tu duda :D}\\&\\&\int_0^3\int_0^12x\sqrt{x^2+y}\ \ dx\ dy\\&\\&\text{Resolamos primero:}\\&\\&\int_0^12x\sqrt{x^2+y}\ \ dx\\&\\&sea \ \ \ u=x^2+y\ \ \ entonces:\ \ \ dx=\frac{du}{2x}\ \ \,  \text{, luego:}\\&\\&\int_0^12x*u^{1/2}\ \frac{du}{2x}=\int_0^1u^{1/2}\ du=\frac{u^{3/2}}{3/2}\Big ]_{0}^{1}=\frac{(x^2+y)^{3/2}}{3/2}\Big ]_{0}^{1}=\frac{(1+y)^{3/2}}{3/2}-\frac{y^{3/2}}{3/2}=\frac{2}{3}*((y+1)^{3/2}-y^{3/2})\\&\\&\text{Luego, sigamos con la segunda parte de la integral:}\\&\\&\\&\end{align}$$

$$\begin{align}&\int_0^3\frac{2}{3}*((y+1)^{3/2}-y^{3/2})\ dy=\frac{2}{3}\int_0^3(y+1)^{3/2}\ dy-\frac{2}{3}\int_0^3y^{3/2}\ dy\\&\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{2}{3}*\frac{u^{3/2+1}}{3/2+1}\Big ]_{0}^{3}-\frac{2}{3}*\frac{y^{3/2+1}}{3/2+1}\Big ]_{0}^{3}\\&\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{2}{3}*(\frac{4^{5/2}}{5/2}-\frac{1^{5/2}}{5/2})-\frac{2}{3}*(\frac{3^{5/2}}{5/2}-0)\\&\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{124}{15}-\frac{12\sqrt{3}}{5}\\&\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =4.10974\\&\\&\end{align}$$

y listo !

Si tienes duda, me preguntas :D

Muchas gracias, solo una duda que tengo finalizando como paso a ser 12raiz de 3/5??

Listo ya recorde: el resultado seria (4√3^5)/15= 4*=12 y 15/3=5 es como reducirlo y a la final nos dara 12√3/5 cierto??

$$\begin{align}&\text{Así es, pasé muy rápido de un paso a otro, una disculpa :D}\\&\\&\text{del ante penúltimo renglón tenemos:}\\&\\&=\frac{2}{3}*(\frac{4^{5/2}}{5/2}-\frac{1^{5/2}}{5/2})-\frac{2}{3}*(\frac{3^{5/2}}{5/2}-0)\\&\\&=\frac{2}{3}*(\frac{2}{5}4^{5/2}-\frac{2}{5})-\frac{2}{3}*\frac{2}{5}3^{5/2}\\&\\&=\frac{4}{15}4^{5/2}-\frac{4}{15}-\frac{4}{15}3^{5/2}\\&\\&=\frac{4*4^{5/2}-4}{15}-\frac{4}{15}\sqrt{3^5}\\&\\&=\frac{4*\sqrt{4^5}-4}{15}-\frac{4}{15}\sqrt{3^2*3^2*3}\\&\\&=\frac{4*\sqrt{4^2*4^2*4}-4}{15}-\frac{4}{15}3*3*\sqrt{3}\\&\\&=\frac{4*4*4*\sqrt{4}-4}{15}-\frac{4}{5*3}3*3*\sqrt{3}\\&\\&=\frac{4*4*4*2-4}{15}-\frac{4*3*\sqrt{3}}{5}\\&\\&=\frac{128-4}{15}-\frac{12*\sqrt{3}}{5}\\&\\&=\frac{124}{15}-\frac{12*\sqrt{3}}{5}\end{align}$$

y eso es todo :D

Cualquier duda, me dices :D