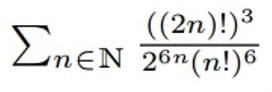Esta serie converge o divege? Usando criterios de convergencia, determinar si la siguiente serie converge o diverge.
Determinar si esta serie es convergente o divergente, usando, ya sea el criterio de D'Alambert o criterio de Cauchy (criterio de la raíz), o el criterio que Ud considere.
1 Respuesta
---
---
¡Hola Claudio!
·
Ya lo intente por el criterio de D'Alambert y tras la simplificación quedaba
$$\begin{align}&\lim_{n\to \infty} \frac{[(2n+2)(2n+1)]^3}{2^6(n+1)^6}\end{align}$$Que yo ya veo que es 1, y si no se ve no hace falta operar mucho para comprobarlo.
Luego lo intentarécon el de Cauchy.
$$\begin{align}&\lim_{n\to \infty} \sqrt[n]{\frac{((2n)!)^3}{2^{6n}(n!)^6}}=\\&\\&\frac {1}{2^6}·\lim_{n\to \infty} \sqrt[n]{\frac{((2n)!)^3}{(n!)^6}}=\\&\\&\text{Usaremos la fórmula de Stirling}\\&\\&n! \approx \sqrt {2\pi n}\left(\frac ne\right)^n\\&\\&=\frac {1}{2^6}·\lim_{n\to \infty} \sqrt[n]{\frac{((2n)!)^3}{(n!)^6}}=\\&\\&=\frac {1}{2^6}·\lim_{n\to \infty} \sqrt[n]{\frac{\left(\sqrt {2\pi 2n}\left(\frac {2n}e\right)^{2n}\right)^3}{\left(\sqrt {2\pi n}\left(\frac ne\right)^n\right)^6}}=\\&\\&\frac {1}{2^6}·\lim_{n\to \infty} \frac{\left(\frac{2n}{e}\right)^6}{\left(\frac ne \right)^6}\sqrt[n]{\frac{\left(2 \sqrt {\pi n}\right)^3}{\left(\sqrt {2\pi n}\right)^6}}=\\&\\&\frac {1}{2^6}·\lim_{n\to \infty}2^6 \sqrt[n]{\frac{2^3}{2^3\left(\sqrt {\pi n}\right)^3}}=\\&\\&=\lim_{n\to \infty} \sqrt[n]{\frac 1{\sqrt{(\pi n)^3}}}\\&\\&\text{Tomamos logaritmos}\\&\\&log (L) =\lim_{n\to\infty}\frac 1n log[(\pi n)^{-3/2}]=\\&\\&\lim_{n\to\infty}-\frac {3·(log\,\pi+log \,n)}{2n}=0\\&\\&Luego\\&\\&L=1\\&\end{align}$$Pues este también da 1, luego no se puede deducir nada.
·
Como último intento usare el criterio de Raabe
$$\begin{align}&\text{Si existe }\lim_{n\to\infty}n\left(1-\frac{a_{n+1}}{a_n} \right)=L\in(-\infty,\infty) \\&\\&\text{Si L>1 converge}\\&\text{Si L<1 diverge}\\&\\&\lim_{n\to\infty}n\left(1-\frac{[(2n+2)(2n+1)]^3}{2^6(n+1)^6} \right)=\\&\\&\lim_{n\to\infty}n\left(1-\frac{(4n^2+6n+2)^3}{2^6(n+1)^6} \right)=\\&\\&\text{Estas cuentas las haré con ordenador}\\&\\&\lim_{n\to\infty}n\left(1-\frac{64n^6+288n^5+528n^4+504n^3+264n^2+72n+8}{64n^6+384n^5+960n^4+1280n^3+960n^2+384n+64} \right)=\\&\\&\lim_{n\to\infty}n\left(\frac{96n^5+432n^4+776n^3+696n^2+312n+56}{64n^6+384n^5+960n^4+1280n^3+960n^2+384n+64} \right)=\\&\\&\lim_{n\to\infty}\left(\frac{96n^6+432n^5+776n^4+696n^3+312n^2+56n}{64n^6+384n^5+960n^4+1280n^3+960n^2+384n+64} \right)=\\&\\&\frac{96}{64}= \frac 32\gt1\\&\end{align}$$Luego el límite existe y es mayor que 1, por el criterio de Raabe(que hay que tener cuidado porque es al revés que los otros dos) la serie es convergente.
---
---
¡Gracias!
Una pregunta, en su criterio de Cauchy, el limite es =0, y pone Ud que es L=1, no entiendo bien. Para Cauchy es L>1 diverge, si L<1 converge, y si L=1, es no concluyente, entonces L=0 0<1 entonces convergería?. Gracias
---
---
No, el límite por Cauchy es 1. Cero es el logaritmo del límite. He llamado L al límite y he calculado su logaritmo neperiano, una técnica que se usa muchas veces. Y una vez calculado, como
log(L) = 0 ==> L=1
Ya veo que no lo expliqué mucho, pero es que si llenas mucho las cajas de lenguaje LaTeX de las fórmulas, el ordenador se para. Por eso casi no hay comentarios y cuando hace falta se tienen que simplificar pasos.
·
Saludos
---
---
