Espero ayudarte:
a) Si tomas el triangulo BDC
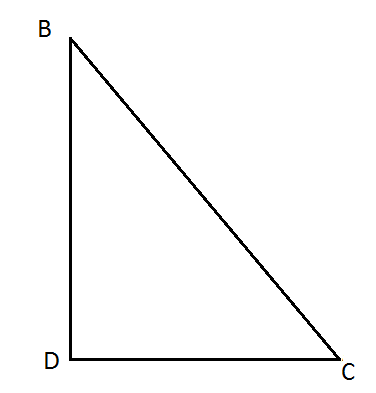 Al ser rectangulo, se puede aplicar el Teorema de Pitagoras, por lo que:
Al ser rectangulo, se puede aplicar el Teorema de Pitagoras, por lo que:
$$\begin{align}&(BC)^2=(BD) ^2+(DC) ^2\end{align}$$ Si analogamente se hace lo mismo con el triangulo ABD
$$\begin{align}&(AB)^2=(BD)^2+(AD)^2\end{align}$$ Pero, AD=DC por lo que
$$\begin{align}&(AB)^2=(BD)^2+(DC)^2\end{align}$$Que es la misma expresion que la inicial (y dado que son longitudes y deben ser positivas)
$$\begin{align}&AB=BC\end{align}$$b) Ya que la semirecta BD es perpendicular a AC, lo convierte en su altura
Si utilizamos triángulos congruentes de acuerdo a sus longitudes, tendremos las igualdades:
$$\begin{align}&AB=BC\\&AD=CD\\&BD=BD\end{align}$$Por lo que se cumplirian las igualdades de los angulos de igual forma, es decir:
$$\begin{align}&ABD=CBD\\&BDA=BDC\\&BAD=BCD\\&\\&\end{align}$$(Perdon, el editor no me permitia colocar el signo de angulo)
Con lo cual BD se convierte en bisectriz del angulo B y se comprueba que los ángulos A y C son iguales (o congruentes)


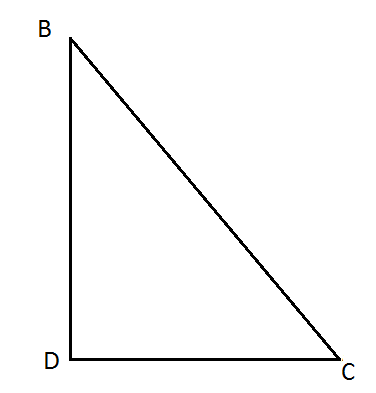 Al ser rectangulo, se puede aplicar el Teorema de Pitagoras, por lo que:
Al ser rectangulo, se puede aplicar el Teorema de Pitagoras, por lo que:
