Como graficar y hallar el dominio de esta función
Que tengo que hacer para encontrar el dominio y graficar esta función
$$\begin{align}&\frac{4-x^2}{2-x}\end{align}$$
1 Respuesta
Hoa Peri Rockz!
Es una función racional (cociente de dos polinomios)
El dominio de una función es el conjunto de valores de la x donde puedo calcular su imagen. En las funciones racionales, cuando das valores a la x, al final tiene que acabar haciendo una división). Todas las divisiones son posibles menos cuando el divisor (denominador de la fracción) vale cero
Luego el dominio de una racional son todos los números reales menos los que anulan el denominador.
En tu caso 2-x=0 ==>x=2
$$\begin{align}&\ Dom= \mathbb {R}- \{ 2 \}\\&\\&Observa \ que \ no \ se \ puede \ calcular \ f(2)=\frac{4-2^2}{2-2}=\frac{0}{0}\\&\\&Para\ hacer \ la \ gráfica \ observa \ la \ simplificación \ de \ la \ fracción:\\&\\&y=\frac{4-x^2}{2-x}=\frac{(2+x)(2-x)}{2-x}=2+x\end{align}$$Que es la ecuación de una recta, que puedes dibujar con una tabla de valores
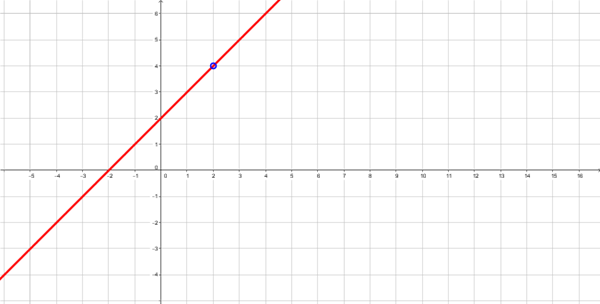
El valor (2, f(2))=(2,4) es un punto de la recta que no existiría en la función original.
Por eso lo he dibujado vacío.
