Dado ∆ABC, es equilátero(AF), (BD) y (CE) son extensiones de los lados del ∆ABC, ∡1≡∡2≡∡3Demuestra que:∆I≡∆II≡∆III
La pregunta es de GeDado ∆ABC, es equilátero
(AF), (BD) y (CE) son extensiones de los lados del ∆ABC, ∡1≡∡2≡∡3
Demuestra que:
∆I≡∆II≡∆III, se trata de un problema de geometría, aquí la imagen que representa el ejercicio.
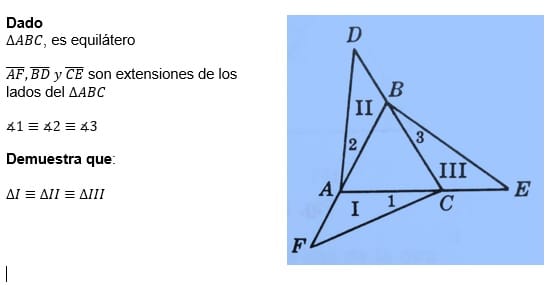
La pregunta es de geometría y se quiere demostrar que los triángulos I, II y III son iguales.
1 Respuesta
Respuesta de Francisco Alvarado
1
Como el ∆ABC es equilátero los ángulos interiores son de 60º.
Los ángulos ∡1≡∡2≡∡3.
Los ángulos ∡FAC≡∡DBA≡∡BCE
Por ser adyacentes suplementarios de ángulos ≡.
Se concluye pues que por medio del criterio de congruencia ALA los
∆i≡∆Ii≡∆iii.
