¿Cómo se resuelve este problema aplicando el método de Simpson?

$$\begin{align}& \end{align}$$

--

--

¡Hola Fer Olvera!

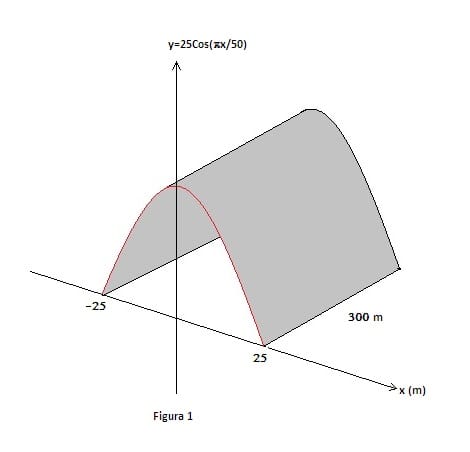
Debemos usar la fórmula de integración del arco de una curva

$$\begin{align}&l=\int_a^b \sqrt{1+(f'(x))^2}dx\\&\\&f(x)=25cos \left(\frac{\pi}{50}x  \right)\\&\\&f'(x)= -\frac{\pi}{2}sen \left(\frac{\pi}{50}x  \right)\\&\\&l=\int_{-25}^{25}\sqrt{1+\frac{\pi^2}{4}sen^2 \left(\frac{\pi}{50}x  \right)}dx\end{align}$$

Para hacer lo siguiente convendría ayudarnos con Excel, no lo tengo aquí, voy a ver si lo puedo hacer con Geogebra que apenas lo manejo

La fórmula de la regla de Simpson para una función f(x) en el intervalo [a, b] es

$$\begin{align}&I=\frac{b-a}{6}\left(f(a)+4f\left(\frac{a+b}{2}  \right)+f(b)  \right)\\&\\&\text{Esto aplicado a n particiones se hace así}\\&\text{Se divide [a,b] en 2n intervalos}\\&a=x_0,x_1,x_2,x_3,...,x_{2n}=b\\&\\&I=\frac{b-a}{6n}\left(f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+...+2f(x_{2n-2})+4f(x_{2n-1})+f(x_{2n})  \right)\\&\\&\text{Que en nuestro caso será:}\\&\\&I=\frac{50}{60}\left(f(x_0)+4f(x_1)+2f(x_2)+4f(x_3)+2f(x_4)+...+2f(x_{2n-2})+4f(x_{2n-1})+f(x_{2n})  \right)\end{align}$$

Luego haremos una tabla que tenga en la primera columna los valores x_i, en la segunda los valores de la función que estamos integrando en ese punto y en la tercera multiplicaremos por 1 e primero y último y desde el segundo al penultimo altenando multiplicaciones por 4 y por 2.

Sumaremos los valores de esa columna C y multiplicaremos el resultado por la constante 5/6

Esta es la tabla:

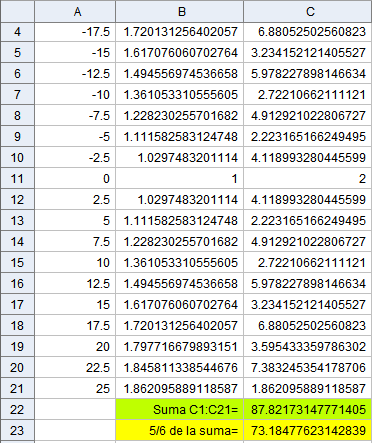
Y esa es la longitud 73.18477623142893

--

--