Una empresa fabrica cortinas para baño, sus costos fijos mensuales ascienden a 20,000 pesos, costos de producción de 20 pesos
Una empresa fabrica cortinas para baño, sus costos fijos mensuales ascienden a 20,000 pesos, costos de producción de 20 pesos por unidad y un precio de venta unitario de 30 pesos. Determine las ecuaciones y funciones de:
- Costos,
- ingresos
- utilidad o
- Si produce y vende 100 cortinas para baño ¿Cuál es su utilidad?
- ¿Qué sucede con las utilidades cuando el valor de POR se acerca a 50 por la derecha?
- ¿Qué sucede con las utilidades cuando el valor de POR se acerca a 50 por la izquierda
- Determine si la función es continua o discontinua
aquí ya trate de resolver una parte pero no se si estoy en lo correcto y todavía no se como resolver de los incisos 5-7 me podrían ayudar esto es lo que tengo al momento
Para calcular costos lo haremos de la siguiente manera
CT=CV+CF
CV=20X donde POR es la cantidad de cortinas producidas
CF=20,000
CT=20X+20,000 esta será la función de costos
Ahora bien para sacar la función de ingreso I usaremos el precio de venta y la incógnita POR quedando de la siguiente manera:
I=30X
Con esta información obtendremos la función de utilidad que queda de la siguiente manera:
U=I-CT
U=30X-(20X+20,000)
U=30X-20X-20,000
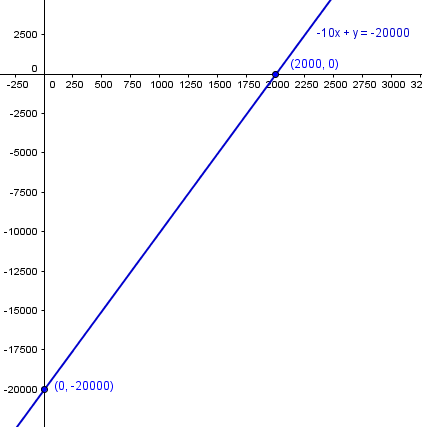
U=10X-20,000
Ahora bien si hay una producción y venta de 100 cortinas que la utilidad de la siguiente manera sustituyendo 100 por POR quedando de la siguiente manera
U=10X-20,000
U=10(100)-20,000
U=100-20,000
U=-19,000
Y como se graficaría esto
1 Respuesta
·
:
¡Hola David!
La función de utilidad es una recta
u(x) = 10x - 20000
es la recta
y=10x -20000
Debes conocer dos puntos para trazarla
Si haces x=0 tienes y=-20000
luego un punto es (0,-20000)
y otro lo puedes conseguir si haces x=2000
y=10·2000 - 20000 = 0
luego el otro punto es (2000,0)
Y esta es la recta.
Cuando se acerca por la derecha el valor es
$$\begin{align}&\lim_{x\to 50^+} 10x-20000=10·50-20000 = -19500\\&\\&\text{y cuando lo hace por la izquierda es}\\&\\&\lim_{x\to 50^-} 10x-20000=10·50-20000 = -19500\\&\end{align}$$Por los dos lados tiene el mismo límite, luego la función es ciontinua en 50. Y puede comprobarse que es continua en cualquier punto. Toda recta es una función siempre continua.
Y eso es todo.
Ok solo una duda
Cuando lo hace por la izquierda es lim
x→50−
¿Cuándo sustituyo por por cincuenta este valor también es positivo o se cambia a negativo?
No.
$$\begin{align}&x\to50^+ \text {significa x tiende a 50 por la derecha}\\&\text{por ejemplo va tomando los valores:}\\&51, \;50.1,\;50.01,\;50.001,\;50.0001,...\\&\\&\text{mientras que } x\to 50^- \text{tiende a 50 por la izquierda}\\&49,\;49.9, \;49.99, \;49.999, ...\\&\\&\text{son siempre números positivos próximos a 50}\end{align}$$Unicamente habría signos distintos cuando se tendiese a 0, entonces ahí por la derecha sería una sucesión positiva y por la derecha negativa, pero cuando se tiende a cualquier otro número las colas de las de las dos sucesiones son del mismo signo.
Luego ese signo + o - de límite por la derecha o la izquierda no significa el signo sino la posición a la derecha o la izquierda del punto del límite. Se podrían haber usado otros símbolos para no confundir pero esos son los que aparecen de siempre en la literatura matremática
Saludos.
·
·
