Como podre realizar estas ecuaciones
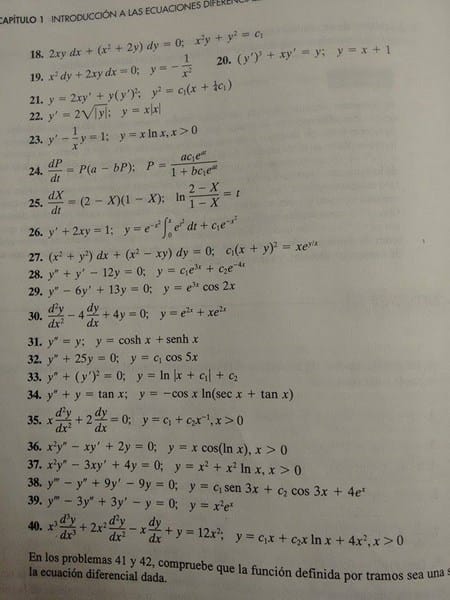
Como sera el correcto procedimiento para realizar las ecuaciones 18 y 19 de estos ejercicios
2 Respuestas
Respuesta de Lucas m
2
Respuesta de Valero Angel Serrano Mercadal
1
