Ecuación de la recta necesito resolver
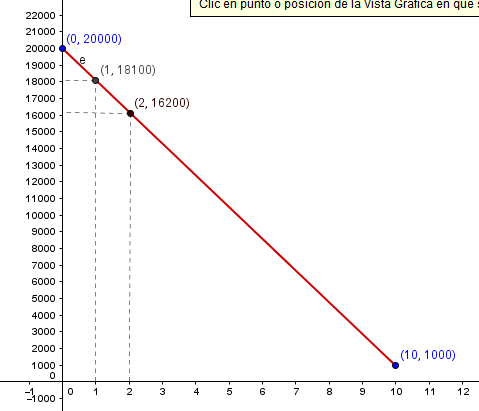
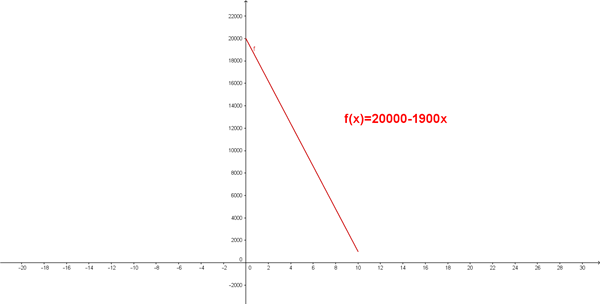
Una empresa adquiere una maquina por un valor de US$ 20.000, el precio de la maquina se desvaloriza hasta su valor de venta es de US$ 1.000 después de 10 anos. Si el precio de la maquina tiene el comportamiento de una recta, exprese el valor de la maquina en el tiempo. Grafique la recta que modela la situación.
2 respuestas
Respuesta de Valero Angel Serrano Mercadal
1
Respuesta de Lucas m
1