·
·
¡Hola Daniela!
3) Se trata de una variable aleatoria continua entre 0 y 2.
Y aunque el que ha hecho el ejercicio quiere que digas que es una función de densidad, ya que la integral es 1, no lo es. No lo es porque una función de densidad es siempre positiva y esta no lo es ya que
f(0) = (2·0-1)/2 = -1/2
Y la función es negativa desde 0 hasta 1/2 luego no es una función de densidad y no se puede continuar, las cuentas que se hicieran serían falsas.
Ten cuidado de exponer bien esto porque estoy seguro de que el profesor no se dio cuenta de ello cuando os mandó el ejercicio.
·
4) Esta sin embargo es siempre positiva ya que 1-x es siempre >=0 al valer 0<=x<=1
a)
Para determinar k haremos que la integral valga 1
$$\begin{align}&1=\int_0^1kx(1-x)^6dx=\\&\\&t=1-x \implies x=1-t\\&dt =-dx\\&x=0\implies t=1\\&x=1\implies t=0\\&\\&=-k \int_1^0 (1-t)t^6 dt=\\&\\&-k\int_1^0(t^6-t^7)dt=\\&\\&-k \left[\frac{t^7}{7}-\frac{t^{8}}{8} \right]_1^0=k \left[\frac{t^7}{7}-\frac{t^{8}}{8} \right]_0^1=\\&\\&k\left(\frac 17-\frac 18\right)=k·\frac {8-7}{56}= \frac{k}{56}\\&\\&luego\\&\frac{k}{56}=1 \implies k=56\\&\\&\text{Y la función será}\\&f(x)=56x(1-x)^6 \quad si\;0\le x\le 1; \quad 0\; si\;no\\&\\&\end{align}$$b)
La gráfica será esta
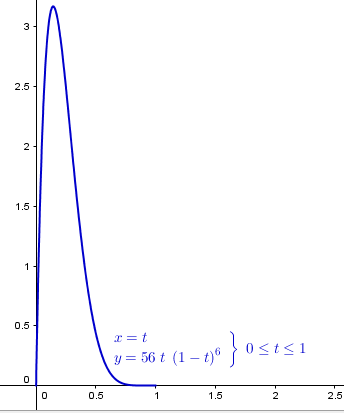
c)
La función acumulada de probabilidad es la integral entre 0 y x. Ya hemos hechos esa integral entre 0 y 1 ahora es un proceso parecido pero no igual del todo.
$$\begin{align}&F(x)=\int_0^x 56u(1-u)^6du=\\&\\&t=1-u \implies u=1-t\\&dt =-du\\&u=0\implies t=1\\&u=x\implies t=1-x\\&\\&=-56 \int_1^{1-x} (1-t)t^6 dt=\\&\\&-56\int_1^{1-x}(t^6-t^7)dt=\\&\\&-56 \left[\frac{t^7}{7}-\frac{t^{8}}{8} \right]_1^{1-x}=56 \left[\frac{t^7}{7}-\frac{t^{8}}{8} \right]_{1-x}^1=\\&\\&56\left(\frac 17-\frac 18-\frac{(1-x)^7}{7}+\frac{(1-x)^8}{8} \right)=\\&\\&8-7-8(1-x)^7+7(1-x)^8 =\\&\\&1 +(1-x)^7(7-7x-8)=\\&\\&1-(1+7x)(1-x)^7\\&\\&\\&F(x) = 1-(1+7x)(1-x)^7\end{align}$$d)
P(X>0.2) = 1 -P(X<0.2) = 1-F(0.2) =
1 - [1 - (1 + 7 ·0.2)(1 - 0.2)^7]= 0.50331648
·
P(X<0.1)= F(0.1) = 1 - (1 + 7 · 0.1)(1 - 0.1)^7 = 0.18689527
·
P(0.2<X<0.4) = F(0.4)-F(0.2) =
1 - (1 + 7 · 0.4)(1 - 0.4)^7 - 1 - (1 + 7 · 0.2)(1 - 0.2)^7=
0.89362432 - 0.49668352 = 0.3969408
:
:


