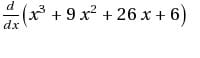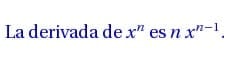Determina la derivada de la función indicada.
Agradezco mucho pudieran asesorarme para resolver esta pregunta en base a esta información:
La función y = x3 + 9x2 + 26x + 6 representa la relación existente entre la cantidad y el costo de las piezas metálicas producidas por DINFUNSA.
○Determina la derivada de la función indicada.
2 Respuestas
Respuesta
1
Respuesta de Valero Angel Serrano Mercadal
1