Dominio y rango de funciones hallarlos

Las parábolas son funciones polinómicas de 2º grado. El Dominio de las funciones polinómicas son todos los reales

Las parábolas (y=ax^2+bx+c) que no tiene término en x (b=0) el vértice cae sobre el eje de ordenadas. Recuerda que el vértice se calcula con la fórmula:

$$\begin{align}&x_v=\frac{-b}{2a}\\&\\&Si   \  \  b=0 \Rightarrow x_v=0\Longrightarrow y_v=f(0)=c\\&\\&\\&1.- \\&a=-1<0 \Rightarrow parábola \ hacia \ abajo \Rightarrow Rc=(- \infty,c)=(\infty,5)\\&\\&x=-1 \Rightarrow f(-1)=4 \Longrightarrow f (1)=4\\&x=-2 \Rightarrow f(-2)=f(2)=1\\&\\&2.- \\&a=1>0  \Rightarrow parábola \ hacia \ arriba  \Rightarrow Rc=(c,+ \infty)=(4,+\infty)\\&f(1)=f(-1)=-3\\&f(2)=f(-2)=0\\&\\&Dom=\mathbb R\end{align}$$

Saludos

:

:

·

·

¡Hola Albert!

Son dos polinomios de grado 2, luego su dominio es todo R.

Dom(-x^2+5) = R

Dom(x^2-4) = R

Y por ser precisamente de grado 2 coinciden los límites en -infinito e infinito y su rango no es todo R. Su rango es el compredido entre el límite que tengan en infinito y el vértice de la parábola.

El vértice de la parábola se puedecalcular con la fórmula

xv=-b/2a

si todavía no has dado máximos y mínimos.

·

Para la función y=-x^2+5 el vértice es

xv= -0/(2·(-1)) = -0/(-2) = 0

y el valor de la función en xv=0 es

-0^2+5 = 5

luego el vértice es (0,5)

Y el límite en infinito es

y = -(inf)^2 + 5 = - inf

Luego el rango es

Rango(-x^2+5) = (-inf, 5]

·

Para la función y = x^2-4 el vértice es

xv = -0/(2·1) = 0

y el valor en ese punto es

0^2-4 = -4

el limite en el infinito es

y = (inf)^2 - 4 = + inf

Rango(x^2-4) = [-4, +inf)

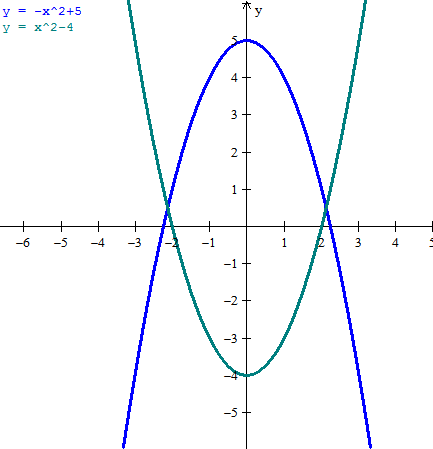
Como puntos puedes tomar aparte de los vértices ya dados los valores de las funciones en cualquier punto por ejemplo en 1

Para y=-x^2+5

x=0 ==> y=5

x=1 ==> y =4

x=2 ==> y = 1

Para y=x^2-4

x=0 ==> y=-4

x=1 ==> y=-3

x=2 ==> y=0

No te he dado ningún valor de x negativo porque la curva por la izquierda es simetrica.

:

: