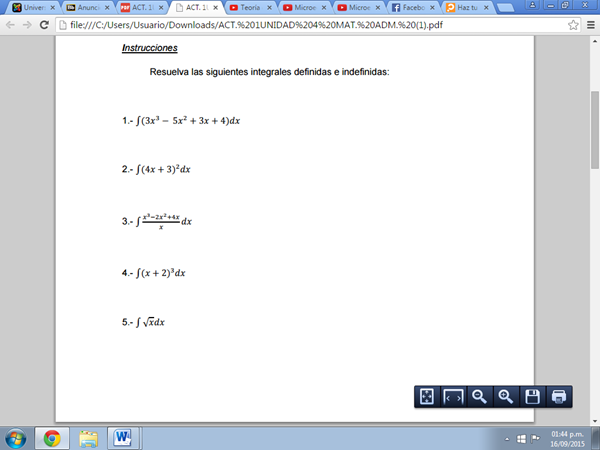
Resuelva las siguientes integrales definidas e indefinidas. Actividad 1. Integral definida y por sustitución
Nuevamente solicitando de la manera más amable su apoyo para la realización de esta actividad de integrales definidas e indefinidas.
1 Respuesta
Respuesta de Valero Angel Serrano Mercadal
1
.
:
¡Hola Melina!
En integrales de esta categoría resolvemos un máximo de dos por pregunta. Contestaré las dos primeras, si quieres las otra mándalas en distintas preguntas tal como digo.
$$\begin{align}&1)\quad \int (3x^3-5x^2+3x+4)dx=\\&\\&\text{se hace en un solo paso, pero con todos es esto}\\&\\&=3\int x^3dx-6\int x^2dx+ 3\int x\,dx+4\int dx=\\&\\&3·\frac{x^4}{4}-6·\frac{x^3}{3}+3·\frac{x^2}{2}+4x+C=\\&\\&\frac 34x^4-2x^3+\frac 32x^2+4x +C\\&\\&--------------------\\&\\&2)\quad \int(4x+3)^2dx=\\&\\&\text{por si no habéis dado el método de sustitución}\\&\\&=\int(16x^2+24x+9)dx=\\&\\&\text{esta vez todo en un paso}\\&\\&=\frac{16}{3}x^3+12x^2+9x +C\end{align}$$:
:
Espera, parece que el título dice que se puede hacer por sustitución, hago el segundo también por sustitución
$$\begin{align}&\int(4x+3)^2dx=\\&\\&t=4x+3\\&dt=4\;dx\implies dx= \frac 14dt\\&\\&=\int t^2·\frac 14dt=\frac 14\int t^2 dt=\\&\\&\frac 14·\frac{t^3}{3}+C = \frac{t^3}{12}+C=\\&\\&\frac{(4x+3)^3}{12}+C\end{align}$$Si desarrollas ese cubo verás que te da lo mismo que antes y aparte un 27/12, pero ese 27/12 se puede pasar a la constante C con lo cual será la misma respuesta que antes.
Saludos.
:
:
