Inecuaciones y desigualdades necesito desarrollar ejercicio

a) Los puntos a considerar es donde la función vale cero y donde la función está indefinida.

Ceros: { -1, 7}

Indefinida: {1, 6, -3}

Ordenando todos los puntos, tenemos que los cambios de signos en la función se dará en los puntos de interés, los puntos ordenados son {-3, -1, 1, 6, 7}

Así que evalúo en los siguientes puntos (solo veré los signos)

$$\begin{align}&-4: \frac{ -\cdot - }{-\cdot  -\cdot  -}=\frac{+}{-} <0\\&-2: \frac{ -\cdot - }{-\cdot  -\cdot +}=\frac{+}{+} >0\\&0: \frac{ +\cdot - }{-\cdot  -\cdot +}=\frac{-}{+} <0\\&2: \frac{ +\cdot - }{+\cdot  -\cdot +}=\frac{-}{-} >0\\&6.5: \frac{ +\cdot - }{+\cdot  +\cdot +}=\frac{-}{+}<0\\&10: \frac{ +\cdot +}{+\cdot  +\cdot +}=\frac{+}{+}>0\\&\text{Por lo tanto los intervalos donde la función es >0 son:}\\&(-3,-1) \cup (1,6) \cup (7,+\infty)\end{align}$$

b) antes conviene operar un poco con esa expresión:

$$\begin{align}&\frac{x}{x-3}\le \frac{x}{x+1}\\&\frac{x}{x-3} - \frac{x}{x+1} \le0\\&\frac{x(x+1)-x(x-3)}{(x-3)(x+1)} \le0\\&Factor\ común...\\&\frac{x(x+1-x+3)}{(x-3)(x+1)} \le0\\&\frac{4x}{(x-3)(x+1)} \le0\\&\text{y ahora planteamos lo mismo que antes:}\\&ceros: {\{0\}}\\&indefiniciones: {\{3,-1\}}\\&Evalúo,\ los\ signos:\\&-2: \frac{-}{- \cdot -}=\frac{-}{+} < 0\\&-0.5: \frac{-}{- \cdot +}=\frac{-}{-} > 0\\&1: \frac{+}{- \cdot +}=\frac{+}{-} < 0\\&4: \frac{+}{+ \cdot +}=\frac{+}{+} > 0\\&\text{Los intervalos de interés son:}\\&(-\infty,-1) \cup [0,3)\\&\\&\\&\\&\end{align}$$

·

·

¡Hola Cintya!

Ejercicios de esta categoría deberías mandar solo uno en cada pregunta.

Se trata de una mera comprobación de signos ya que son varios factores multiplicando o dividiendo en la izquierda, un signo mayor y un 0 a la derecha. Hay que comprobar si el signo de la izquierda es positivo. Y en un producto el resultado es positivo cuando el número de factores negativos es par.

Si ordenamos las raíces de los factores tendremos

{-3, -1, 1, 6, 7)

El el intervalo (-inf, -3) son todos los factores negativos, como son 5 el resultado es negativo y no sirve.

En cada intervalo que vayamos avanzando hay un factor negativo menos

(-3, -1) hay 4 negativos, resultado positivo, sirve

(-1, 1) hay 3 negativos, resultado negativo, no sirve

(1,6) hay 2 negativos, resultado positivo, sirve

(6,7) hay un negativo, resultado negativo, no sirve

(7, inf) hay cero negativos, resultado positivo, sirve.

Notese que no sirva ninguna de las raices, las del denominador por no estar definida la función y las del numerador por ser una desigualdad estricta

Luego la solución es:

$$\begin{align}&S=(-3,-1)\cup (1,6)\cup (7,\infty)\end{align}$$

·

b)

Lo pasaremos todo a un sitio para que el ejercicio se transforme en una comprobación de signos

$$\begin{align}&\frac{x}{x-3}\le \frac{x}{x+1}\\&\\&\frac{x}{x-3}-\frac{x}{x+1}\le 0\\&\\&\frac{x(x+1)-x(x-3)}{(x-3)(x+1)}\le 0\\&\\&\frac{x^2+x-x^2+3x}{(x-3)(x+1)}\le 0\\&\\&\frac{4x}{(x-3)(x+1)}\le 0\\&\\&\text{los puntos donde algún factor cambia de signo son:}\\&\\&\{-1,0,3\}\\&\\&\text{Dividiendo por zonas}\\&\\&(-\infty, -1) \text{ son tres negativos, resultado negativo, sirve}\\&(-1,0)\text{ son dos negativos resultado positivo, no sirve}\\&(0,3)  \text{ hay 1 negativo, resultado negativo, sirve}\\&(3,\infty) \text{son todo positivos, resultado positivo, no sirve}\\&\\&\text{Aparte sirve el 0 y -1 y 3 no sirven por no estar definida}\\&\\&\text{Luego la solución es:}(-\infty,-1)\cup[0,3)\end{align}$$

Y no está de más comprobar con algún programa de gráficas, la solución será las zonas donde la función es negativa.

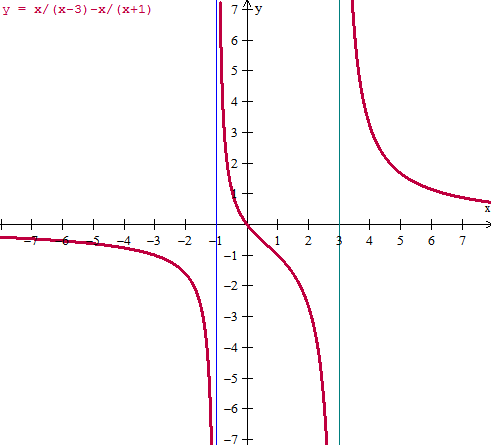
Vale, está bien.

Saludos.

:

.