Como resuelvo este ejercicio de polinomios?

Te hago los otros dos, aprovechando la explicación del profesor Valero:

c) f(x)=x^3-2x^2++x+1 ===> f(0)=1

g(x)= -2x^2+x+1  ===> g(0)=1

f(x)'=3x^2-4x+1  ===> f(0)'=1

g(x)'=-4x+1  ===> g(0)'=1

f(x)''=6x-4 ===> f(0)''=-4

g(x)'' =-4

f(x)'''=6  distinta de g(x)'''=0

De orden 2

d) f(x)=x^4+x^3+x^2+5 ===> f(-2)=16-8+4+5=17

g(x)= -2x^3+1 ===> g(-2)=16+1= 17

f(x)'=4x^3+3x^2+2x  ===> f(-2)'=-32+12-4= -24

g(x)'=-6x^2  ===>  g(-2)'=-24

f(x)''=12x^2+6x+2  ===> f(-2)''=48-12+2=38

g(x)''=-12x  ===> g(-2)''=24    

De orden 1

Saludos

:

:

·

·

¡Hola Mauricio!

EL orden de contancto indica cómo sob de parecidas dos curvas en un punto donde se cortan.

Contacto de orden 0 sería simplemente que se cortan, pero la derivada es distinta.

Contacto de orden 1 sería cuando se cortan y la derivada primera es la misma, pero la segunda distinta.

Y en general, tienen contacto de orden n si coinciden las funciones y las derivadas hasta la enésima y la derivada n+1 es distinta

Haré alguno para que lo veas

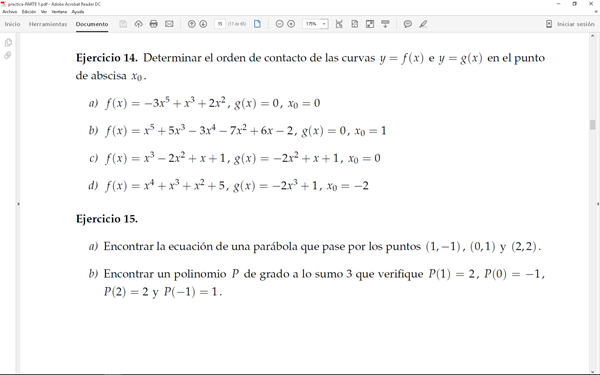
a)

f(x) = -3x^5+x^3+2x^2

g(x) = 0

en xo=0

Comprobamos fácilmente que el valor es es mismo f(0) = g(0) = 0

Calculamos la derivada primera

f'(x) = -15x^4 + 3x^2 + 4x

g'(x) = 0

Comprobamos que f'(0)=g'(0)=0

Calculamos la derivada segunda

f''(x) = -50x^3 + 6x + 4

g''(x) = 0

Y aquí vemos que f''(0) = 4  y g''(0) = 0

Luego han coincidido hasta la primera, el orden de contacto es 1.

·

b)

f(x) = x^5 + 5x^3 - 3x^4 - 7x^2 + 6x - 2

g(x)= 0

en xo=1

veamos los valores de las funciones en x=1

f(1) = 1+5-3-7+6-2= 0

g(1) = 0

tenemos f(1)=g(1)=0

Calculamos las derivadas primeras

f'(x) = 5x^4 +15x^2 - 12x^3 - 14 x + 6

f'(1) = 5 + 15 - 12 -14 + 6 = 0

g'(1) = 0

coindicen f'(1)=g'(1)

Calculamos las derivadas segundas

f''(x) = 20x^3 + 30x - 36x^2 - 14

f''(1) = 20+30-36-14=0

g''(1)=0

luego f''(1)=g''(1)

Calculamos las terceras

f'''(x) = 60x^2 +30 -72x

f'''(1) = 60+30-72 = 18

g'''(1) = 0

Aquí ya son distintas. Luego fueron iguales hasta la segunda, el orden de contacto es 2.

·

Y eso es todo, puedes terminar fácilmente los que quedan o mándalos en otra pregunta.

Saludos.

::

: