Hay solución para este paralelogramo?
Su apoyo por favor con lo siguiente: en el paralelogramo ABCD, AE corta a la diagonal BD en G y DC en F. Si AG= 6 cm, y GF = 4 cm, ¿cuánto mide EF?
2 respuestas
Los triángulos ABE y FCE son semejantes (estan en posición de Thales)
Luego se cumple la proporción:
$$\begin{align}&\frac{AB}{FC}=\frac{AE}{FE}\\&\\&Sea \ \ AB=a \ \ y \ \ FE=x\\&\\&\frac{a}{FC}=\frac{6+4+x}{x}=\frac{10+x}{x}\end{align}$$Los triángulos ABG i FDG son semejantes ya que angulo G común y
A=F y B=D
luego se cumple la proporción :
$$\begin{align}&\frac{AB}{FD}\frac{AG}{FG} \Rightarrow \frac{a}{FD}=\frac{6}{4} \Rightarrow \frac{a}{a-FC}=\frac{6}{4}\Rightarrow4a=6a-6FC\\&\\&\Rightarrow2a=6FC \Rightarrow a=3FC \Rightarrow \frac{a}{FC}=3\\&\\&Sustituyendo \ en \ la \ primera \ proporción:\\&\\&3=\frac{10+x}{x}\\&\\&3x=10+x\\&2x=10\\&x=5\\&\\&FE=5\\&\\&\end{align}$$Saludos
:
:
Vaya, !
¿No lo entendiste?
Espero que el profe Valero Angel Serrano Mercadal te pueda resolver el ejercicio analíticamente ya que no le encuentro la vuelta :). Yo lo resolví con GeoGebra y te anticipo que la respuesta es 5. Pero desde ya que esto no podrás utilizarlo para demostrar cuanto vale.
Te dejo una imagen y te digo como fui construyendolo:
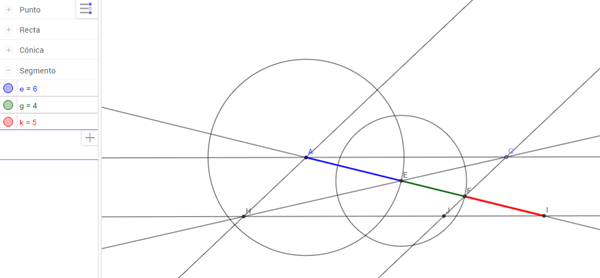
1. Recta horizontal que pasa por A
2. Trazar una oblicua a partir de A (con una pendiente cualquiera y es la que contendrá los 3 segmentos en análisis
3. Con compás, a partir del punto A marcar 6 para ver donde corta la oblicua (en el punto E)
4. A partir del punto E, marcar con compás nuevamente 4 centímetros con la oblicua (punto F)
5. Trazar otra oblicua con otra inclinación que pase por el punto F (será el lateral derecho del paralelogramo), hasta que corte la recta original (en el punto G)
6. Trazar una paralela a la recta anterior, que pase por el punto A
7. Trazar el segmento GE y extenderlo hasta que corte la recta anterior (en el punto H)
8. Trazar una horizontal (paralela a la primer recta) que pase por el punto H
9. Donde se corte esta última recta horizontal, con la oblicua del punto 2 queda determinado el punto I
10. Medir el segmento FI