Realiza la resolución de Desigualdades
Resuelve la siguiente desigualdad (5-x)/2 -(x-17)/4 ≥ x/3-(7x-3)/12
Resuelve por el método gráfico la desigualdad -3x2>2x-1
1 Respuesta
Respuesta
1
Veamos...
$$\begin{align}&1) \frac{5-x}{2}-\frac{x-17}{4}\ge \frac{x}{3}-\frac{7x-3}{12}\\&Factor\ común\\&\frac{10-2x-x+17}{4}\ge \frac{4x-7x+3}{12}\\&Opero\ y\ paso\ restando\\&\frac{-3x+27}{4} - \frac{-3x+3}{12}\ge 0\\&Factor\ común\\&\frac{-9x+81+3x-3}{12}\ge 0\\&Opero\\&\frac{-6x+78}{12}\ge 0\\&-6x+78 \ge 0\\&6(-x+13) \ge 0\\&-x+13 \ge 0\\&13 \ge x\\&\\&\\&\end{align}$$2)
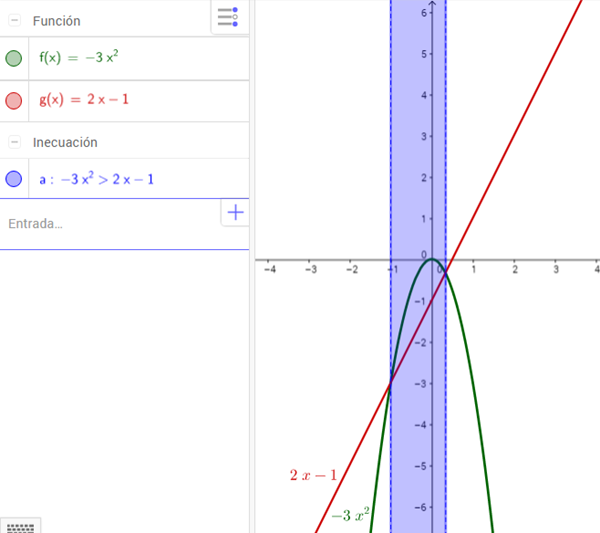
En la imagen se ve fácilmente que uno de los límites es x=-1, el que no está muy claro es el otro, pero si reacomodás la desigualdad te queda
-3x^2-2x+1 > 0
Y acá podés aplicar la resolvente para la cuadrática o Ruffini sabiendo que una de las raíces es x=-1 para obtener que el otro valor es x=1/3
Por lo tanto la respuesta es x pertenece (-1, 1/3)
¡Gracias! profe por su apoyo, disculpen no sé si es mucho pedir, que me oriente en cuanto a los axiomas de los números reales utilizados?