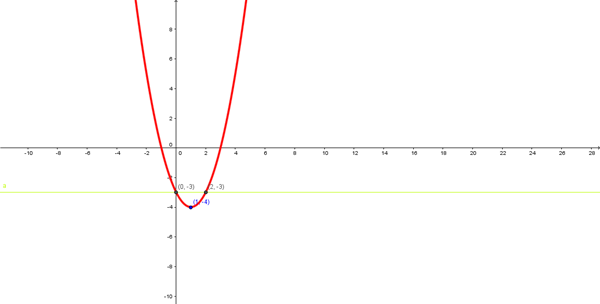
b) No es inyectiva, ya que excepto el vértice, dos elementos distintos de x tienen la mis imagen, por ejemplo f(0)=f(2)=-3. Si al dibujar una paralela al eje X cortas la gráfica en más de un punto no es inyectiva
c) No es sobreyectiva ya que valores de y<2 no tienen imagen.
Una función es supreyactiva cuando el Codominio y el Recorrido don iguales. Como el recorrido de esta función es [2,+infinito)
Para que fuera suprayectiva habría que redefinir la función
$$\begin{align}&f: \mathbb R \longrightarrow [2,+ \infty)\end{align}$$d) como no és inyectiva no tiene función inversa. La relación inversa en realidad son dos funciones una para la rama decreciente de la parábola, y otra para la rama creciente.
Para calcular la inversa cambiamos x por y en la función dada y despejamos la nueva y:
$$\begin{align}&y=x^2-2x-3\\&\\&x=y^2-2y-3\\&\\&y^2-2y-(3+x)=0\\&\\&y=\frac{2 \pm \sqrt{4+4(3+x)}}{2}\\&\\&y_1=\frac{2+ \sqrt{16+x}}{2}\\&\\&y_1=\frac{2- \sqrt{16+x}}{2}\end{align}$$d) f(2)=-3
Saludos
;
;

