Como Graficar función de calculo

Te explico el orden lógico de hacer las cosas.

1.- El Dominio:

Es una función racional, el dominio son todos los puntos menos los que anulan el denominador:

$$\begin{align}&x^2-1=0 \Rightarrow x=\pm1\\&\\&Domf(x)=\mathbb R-  \ { -1,1 }\\&\\&2.- corte \ eje X \Rightarrow y =0 \Rightarrow \frac{x}{x^2-1}=0 \Rightarrow x=0\\&Pasa  \ por \ el \ origen \ de \ coordenadas:(0,0)\\&corte\ eje \ Y \Rightarrow x=0\\&f(0)=\frac{0}{-1}=0\\&\\&3.-Simetría:\\&f(-x)=\frac{-x}{x^2-1}\\&\\&-f(x)=-\frac{x}{x^2-1}\\&luego \Rightarrow f(-x)=-f(x)   \ función \ \ impar ( \ simétrica \ respecto \ el\ Origen \ de  \ coordenadas)\\&\\&4.- Asíntotas Verticales:\\&\\&\lim_{x \to  \pm1} \frac{x}{x^2-1}=\frac{\pm 1}{0}= \infty\\&\\&x=1 \\&x=-1\\&\\&Asíntotas \ horizontales:\\&\lim_{x \to \pm \infty}f(x)=0 \Rightarrow y=0 \ (eje  \  X \  es \ Asíntota \ horizontal)\\&\\&\end{align}$$

5.- Intervalos de Crecimiento:

Se han de ordenar los Puntos críticos (y'=0) y los puntos de discontinuidad (Asint Verticales)

$$\begin{align}&y'=\frac{1(x^2-1)-x·2x}{(x^2-1)^2}=\frac{x^2-1-2x^2}{(x^2-1)^2}=\frac{-x^2-1  }{(x^2-1)^2}\\&\\&y'=0 \Rightarrow \frac{-x^2-1  }{(x^2-1)^2}=0 \Rightarrow -x^2-1=0 \Rightarrow x^2=-1 \ \sin \ solución\\&\end{align}$$

No hay puntos críticos. Los intervalos de crecimiento  se construyen con las Asintotas Verticals:dos A.V implica tres intervalos:

$$\begin{align}&(-\infty,-1) \Rightarrow f'(-10)=\frac{-101}{+}=-(decreciente)\\&\\&(-1,1) \Rightarrow f'(0)=\frac{-1}{+}=-  (decreciente)\\&\\&(1,+\infty) \Rightarrow f'(10)=\frac{-101}{+}<0 (decreciente)\\&\end{align}$$

6.- Intervalos de Concavidad-Conexidad.

Se construyen con los puntos que anulan la derivada segunda, y con los puntos de discontinuidad (A.V)

$$\begin{align}&y'=\frac{-x^2-1}{(x^2-1)^2}\\&\\&y''=\frac{-2x(x^2-1)^2-(-x^2-1)·2·(x^2-1)2x}{(x^2-1)^4}=simplificando\\&\\&=\frac{-2x(x^2-1)+(x^2+1)4x}{(x^2-1)^3}=\frac{2x^3+6x}{(x^2-1)^3}\\&\\&y''=0 \Rightarrow \frac{2x^3+6x}{(x^2-1)^3}=0 \Rightarrow 2x^3+6x=0 \Rightarrow 2x(x^2+3)=0\\&\\&\Longrightarrow\\&2x=0  \Rightarrow x=0\\&\\&x^2+3=0  \rightarrow x^2=-3 (\sin \ solucion)\\&Intervalos  Concavidad:\\&(-\infty,-1) \rightarrow f''(-10)<0(comprobarlo)\\&\\&(-1,0) \rightarrow f''(-1/2)>0\\&(0,1) \rightarrow f''(1/2)<0\\&(1,+\infty) \rightarrow f''(10)>0 \end{align}$$

Los intervalos donde la y''>0 es cóncava o hacia arriba

y''<0 convexa o hacia abajo

El punto (0,0) es un Punto de Inflexión

Graficando

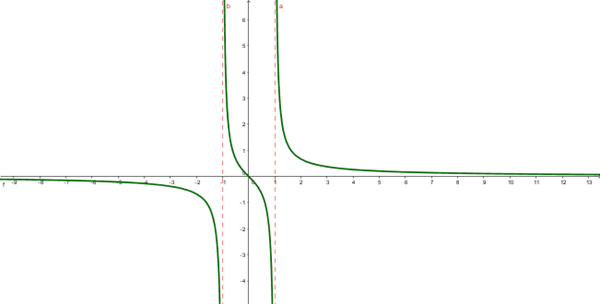
Observa que la función es siempre decreciente

Saludos

:

: