Tengo dudas respecto a Funciones parte III

·

·

¡Hola Marco!

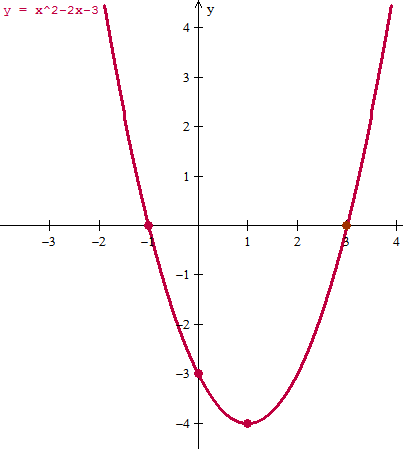
Yo no sé si habrás dado ya derivadas que es algo que se utiliza para representar gráficas. Por si no lo has dado lo haremos sin ellas

Es un polinomio, luego está definida en todo R y es continua.

Los cortes con el eje X son

x^2 - 2x - 3 = 0

Yo veo claramente que eso se factoriza así

(x-3)(x+1) = 0

luego los cortes son en x=3  y x =-1

El corte con el eje Y es

y=0^2 - 2·0 - 3 = -3

Y otro dato importante en una parábola es el vértice, cuya coordenada x se calcula así

x = -b/2a

donde la ecuación sería ax^2 + bx + c = 0

luego la coordenada x del vértice es

x=-(-2)/2 = 1

y el valor de y en esa coordenada x es

y= 1^2 - 2·1 - 3 = 1 - 2 - 3 = -4

luego el vértice es (1, -4)

Y con estos cuatro puntos y alguno más si necesitaras se dibuja la curva.

b) No es inyectiva. Sin ir más lejos ya calculamos antes que

f(-1)=f(3)=0

Cuando alguna línea horizontal corta a la curva en dos punto ya no es inyectiva.

c) No es sbreyectiva ya que los valores yo con yo<-4 no tienen ningún valor xo tal f(xo)=yo

El rango de la función es

Rango f = [-4, infinito)

La solución es hacer que la función sea una función de R en ese rango calculado, es decir

f:  R ----> [-4, infinito)

    x -----> x^2 - 2x - 3

·

d)

Hay que despejar x. Luego se cambia la y por x en la derecha y a la izquierda x por f^-1(x)

$$\begin{align}&y=x^2-2x-3\\&\\&x^2-2x-3-y=0\\&\\&x=\frac{2\pm \sqrt{4+4(3+y)}}{2}\\&\\&x=1\pm \sqrt{4+y}\\&\\&f^{-1}(x)= 1\pm \sqrt{4+x}\\&\\&\\&\\&e)\\&\\&(f\circ f)(2)=f(f(2))=\\&f(2^2-2·2-3) =f(4-4-3)=\\&f(-3)=(-3)^2-2·(-3)-3=9+6-3=12\\&\\&Resumiendo\\&(f\circ f)(2) = 12\end{align}$$

:

: