Ejercicio investigación de operaciones método gráfico
No sé como solucionar el siguiente ejercicio:
1 respuesta
·
·
¡Hola Mila!
No dices cuál es la pregunta, aunque supongo que es maximizar las utilidades.
En principio la cantidad de melaza es fija y su utilidad será:
4000 · 0.1 · 35 = $14000
La azucar morena inicial es:
AM = 4000 · 0.3 = 1200 Tn
la azucar blanca será
AB = 0.8·(AM destinado a AB)
Y el azúcar glas será
AG = 0.95·(AB destinado a AG)
Si llamamos
x = toneladas de azúcar morena
y = toneladas de azucar blanca
z = toneladas de azucar glas tendremos
x + y/0.8 + z/(0.8·0.95) = 1200
x + 1.25 y + (25/19)z = 1200
x puede tomar valores entre 25 Tn y
1200 - 1.25·25 - (25/19)·25 = 86325/76 = 1135.855263 Tn
y puede tomar valores entre 25 y
[1200 - 25 - (25/19)·25] / 1.25 = 17360/19 = 913.6842105 Tn
z los puede tomar entre 25 Tn y
[1200 - 25 - 1.25·25] / (25/19) = 3477/ 4 = 869.25 Tn
La función de utilidad será
U = 150x + 200y + 230z + 14000
Pero dada la relación que tienen entre ellas la podemos reducir a dos variables, por ejemplo si despejamos x aquí
x + 1.25y + (25/19)z = 1200
x = 1200 - 1.25y - (25/19)z
la función de utilidad será
U = 180000 - 187.5y - (3750/19)z + 200y + 230z +14000
U = 194000 + 12.5y + (620/19)z
Pero aun debemos establecer unos límites para la suma de y con z, ya que si no podríamos pasarnos del material disponible.
x + 1.25y + (25/19)z = 1200
como x >=25
1.25y + (25/19)z <= 1175
Resumiendo:
La función objetivo es
U = 194000 + 12.5y + (620/19)z
y las restricciones son
y >= 25
y <= 17360/19
z>=25
z <= 3477/4
1.25y + (25/19)z <= 1175
Solo es cuestión de hacer la gráfica. Ya te anticipo que va a ser un poco liosa porque el programa de gráficas me obliga a llamar (x, y) a las variables y yo las tenía (y, z), luego he hecho y=x, z=y
Y después tu puedes escribir las ecuaciones de las rectas de una forma que el programa las transforma a su manera, de todas forma pienso que podras identificarlas.
Como puedes ver sobran los límites superiores de las dos variables, ya que la recta que las limita conjuntamente es suficiente para delimitar la región factible.
Y trazamos la recta de la función objetivo con constante 0 (en marrón) y buscamos la paralela que esté más eljana y pase por algún punto de la región factible.
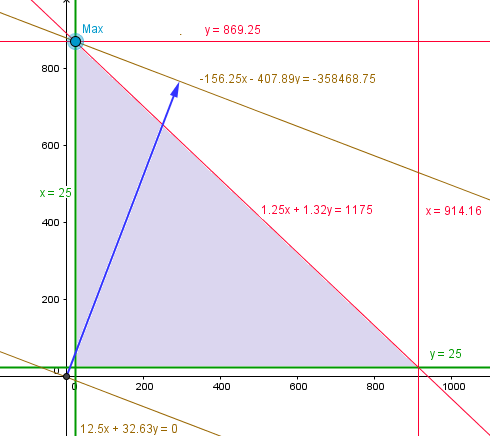
Y el punto que da la máxima utilidad es (y, z) = (25, 869.25)
Solo nos falta calcular el valor de x
x = 1200 - 1.25y - (25/19)z = 1200 - 31.25 - 1143.75 = 25
Luego la utilidad máxima se consigue con:
Azúcar morena = 25 Tn
Azúcar blanca = 25 Tn
Azucar glas = 869.25 Tn
Melaza = 400 Tn
Utilidad = 25·150 + 25·200 + 869.25·230 + 400·35 = $222677.5
Está bien claro, el azucar glas es lo más rentable y se debe producir todo lo que se pueda salvo las 25 obligadas de morena y blanca y las inevitables 400 de melaza.
:
:
