Hallar la ecuación del lugar geométrico del centro de una circunferencia

·

·

¡Hola Lola!

Si es tangente a la recta, la distancia del centro a la recta será el radio

$$\begin{align}&\text{Sea la circunferencia con ecuación}\\&\\&(x-h)^2+(y-k)^2=r^2\\&\\&\text{sabemos que C(h,k) es el centro}\\&\\&d(C,recta) = \frac{|k-1|}{\sqrt{0^2+1^2}}=|k-1|=r\\&\\&\text{Luego la ecuación de la circunferencia queda}\\&\\&(x-h)^2+(y-k)^2=|k-1|^2\\&\\&x^2-2hx+h^2+y^2-2ky+k^2= k^2-2k+1\\&\\&x^2+y^2 -2hx -2ky +h^2+2k-1=0\\&\\&\text{Y la intersección de esta circunferencia con }\\&\\&x^2+y^2=9\\&\\&\text{debe ser un punto único.}\\&\\&\text{Sustituyendo esta en la anterior}\\&\\&9 - 2hx \pm 2k \sqrt{9-x^2} +h^2+2k-1=0\\&\\&\pm2k \sqrt{9-x^2}=-8+2hx-h^2-2k\\&\\&4k^2(9-x^2) = 4h^2x^2 -2(2hx)(8+h^2+2k)+(8+h^2+2k)^2\\&\\&4(h^2+k^2)x^2-4h(8+h^2+2k)x+(8+h^2+2k)^2-36k^2=0\\&\\&\text{Para que haya solucion única el discriminante debe ser 0}\\&\\&16h^2(8+h^2+2k)^2-16(h^2+k^2)[(8+h^2+2k)^2-36k^2]=0\\&\\&16·36h^2k^2-16k^2[(8+h^2+2k)^2-36k^2]=0\\&\\&16·36k^2(h^2+k^2) - 16k^2(8+h^2+2k)^2=0\\&\\&36(h^2+k^2)-(8+h^2+2k)^2=0\\&\\&\end{align}$$

Y como esto ha sido algo complicado haré la gráfica para asegurarme de que es posible que sea esa la respuesta.

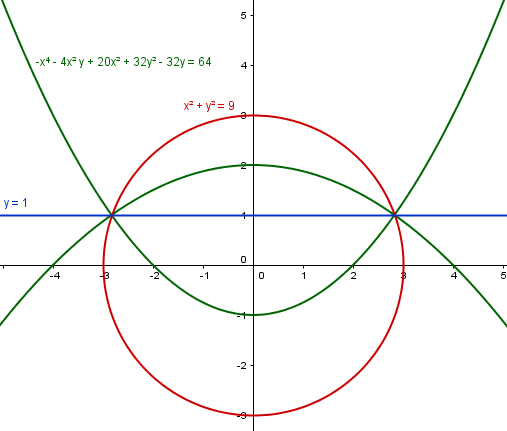
Perfecto, más perfecto imposible. Como ves se trata de dos curvas que podremos obtener descomponiendo la curva en dos factores.

$$\begin{align}&36(h^2+k^2)-(8+h^2+2k)^2=0\\&\\&\left(6 \sqrt{h^2+k^2}+8+h^2+2k\right)\left(6 \sqrt{h^2+k^2}-8-h^2-2k\right)=0\\&\\&\text{Y son estas dos curvas:}\\&\\&6 \sqrt{h^2+k^2}+8+h^2+2k=0\\&6 \sqrt{h^2+k^2}-8-h^2-2k=0\end{align}$$

Que aunque a simple vista puedan parecer parábolas, no lo son.

Y so es todo, espero que te sirva y lo hayas entendido.

Saludos.

·

·

:

:

De dónde sale esta ecuación:  -x⁴ - 4x² y + 20x² + 32y² - 32y = 64 ?

¡Ah! Supongo que para terminar el ejercicio del todo en vez de usar las variables h, k habría que usar la variables x, y para la expresión del lugar geométrico, entonces h era la "x" y k era la "y".

Con ello quedaría la expresión:

$$\begin{align}&36(x^2+y^2)-(8+x^2+2y)^2=0\\&\\&\text{Que equivaldria a estas dos curvas:}\\&\\&6 \sqrt{x^2+y^2}+8+x^2+2y=0\\&6 \sqrt{x^2+y^2}-8-x^2-2y=0\\&\\&\text{En el programa de gráficas yo introduje}\\&36(x^2+y^2)-(8+x^2+2y)^2=0\\&\\&\text{pero al programa le gusta dejarlo a su manera}\\&\text{y efectúa los paréntesis}\\&\\&36x^2+36y^2 -(64+x^4+4y^2+16x^2+32y+4x^2y)=0\\&\\&36x^2+36y^2 -64-x^4-4y^2-16x^2-32y-4x^2y=0\\&\\&-x^4-4x^2y+20x^2+32y^2-32y=64\\&\\&\\&\end{align}$$

Ahí está la explicación a tu pregunta.

Probablemente sea esta la respuesta que más le guste al profesosr ya que es la que lleva más trabajo. Pero todo es cuestión de gustos, yo me habría quedado con la que no está desarrollada.

Saludos.

:

:

¡Gracias! Fue de mucha ayuda!