Como estudiar y trazar las curvas de las siguientes funciones?
Estudia y traza las curvas de;
a) f(x)=x/x2^+1
b) x2^-1/x+3=f(x)
2 Respuestas
Cuando uses operadores que tienen distinta precedencia debes usar paréntesis para que estemos seguro de que función se trata. Además estás usando el operador ^ (elevado a) pero luego lo sigues con un signo de suma o resta y no se entiende que quieres decir. Confirma si las funciones que quieres son:
$$\begin{align}&a) f(x) = \frac{x}{x^2+1}\\&b) f(x) = \frac{x^2-1}{x+3}\end{align}$$
Sí! son esas.
Ok, como la primera ya te la resolvió el profe Valero, y además las funciones son ejercicios muy largos de realizar, voy a hacer solo la segunda
$$\begin{align}&f(x) = \frac{x^2-1}{x+3}\\&\text{La función no está definida cuando el denominador es cero, luego}\\&Dom: R - \{-3\}\\&f'(x) = \frac{2x}{x+3}-\frac{x^2-1}{(x+3)^2}=\frac{2x(x+3)-(x^2-1)}{(x+3)^2}=\frac{x^2+7}{(x+3)^2}\\&P. Críticos \ (f'(x)=0)\\&f'(x)=0 \to 0 = \frac{x^2+7}{(x+3)^2}\\&x^2+7=0 \to x^2 = -7 \to x=\sqrt{-7} \Rightarrow \nexists \ p. críticos\\&Signo\ de\ f'(x)\\&Numerador: \ siempre\ positivo\\&Denominador: \es\ un\ cuadrado\ así\ que \ también \ es\ positivo\\&\Rightarrow f'(x) >0\\&f''(x) =\frac{2x}{(x+3)^2}+\frac{-2(x^2+7)}{(x+3)^3}=\frac{2x(x+3)-2x^2-14}{(x+3)^3}=\frac{-8}{(x+3)^3}\\&f''(x) \ne 0 \ (\forall x)\\&\text{Veamos signo de f''(x)}\\&f''(x<-3) =\frac{-}{-}=+ \ concava\ hacia \ abajo\\&f''(x>-3) =\frac{-}{+}=- \ concava\ hacia \ arriba\\&Asintotas:\\&\text{Verticales: ya vimos que x=-3 es asíntota vertical}\\&\lim_{x \to -3} \frac{x^2-1}{x+3}=\infty\\&\lim_{x \to -3^-} \frac{x^2-1}{x+3}=-\infty\\&\lim_{x \to -3^+} \frac{x^2-1}{x+3}=+\infty\\&Horizontal:\\&\lim_{x \to \infty} \frac{x^2-1}{x+3}=\infty\\&\text{Oblicuas: al no haber horizontales, analizamos esto, sí y=mx + b}\\&m=\lim_{x \to \infty} \frac{f(x)}{x}=\lim_{x \to \infty} \frac{x^2-1}{x(x+3)}=\lim_{x \to \infty} \frac{x^2-1}{x^2+3x}=1\\&b=\lim_{x \to \infty} (f(x) - mx)=\lim_{x \to \infty} \frac{x^2-1}{x+3}- 1\cdot x=\\&\lim_{x \to \infty} \frac{x^2-1-x(x+3)}{x+3}=\lim_{x \to \infty} \frac{x^2-1-x^2-3}{x+3}=\\&\lim_{x \to \infty} \frac{-4}{x+3}=0\\&\therefore asintota \to y = x\end{align}$$Te dejo la imagen de la función
·
·
¡Hola Sia!
La funciones están mal escritas, supongo que has querido poner
a) f(x) = x/x^2+1
b) f(x) = x^2-1/x+3
El símbolo de esponente ^debe ir antes del exponente.
Y además creo que no has tenido en cuenta que los numeradores o numeradores que tiene operaciones dentro deben ir entre paréntesis, de forma que creo que lo que finalmente deberías haber escrito es:
a) f(x) = x / (x^2+1)
b) f(x) = (x^2-1) / (x+3)
Voy a hacer el primero, el estudio de un afunción y gráfica es un ejercicio largo.
a)
f(x) = x/(x^2+1)
El dominio es todo R salvo cuando el denominador sea 0
x^2 + 1 = 0
x^2 = -1
no tiene soluciones reales luego el denominador no es 0 nunca
Dom f = R
·
Continuidad.
Es una función racional (cociente de polinomios) es continua en todos los puntos salvo cuando el denominador es 0. Ya vimos antes que no existen esos valores, luego la función es continua en todo R
·
Cortes con los ejes:
Con el eje X cuando f(x)=0
x/(x^2+1) = 0 ==> x= 0
Luego es el punto (0,0)
Con el eje Y cuando x=0
f(0) = 0 / (0+1) = 0
Da el punto (0,0) que es el mismo que ya teníamos
·
Asíntotas.
Vertical si para algún punto la función tiende a infinito. No hay ninguna, la habría si en algún punto el denominador fuera 0, pero no lo hay.
Horizontal si el límite en el infinito es finito
lim x-->inf [x/(x^2+1)] = 0
Es el mismo límite en -infinito y +infinito
Luego hay una asíntota horizontal y=0
Oblicua, es incompatible con la horizontal, luego no existe.
·
Puntos críticos.
$$\begin{align}&f(x) = \frac{x}{x^2+1}\\&\\&f'(x) = \frac{x^2+1-2x^2}{(x^2+1)^2}=\frac{-x^2+1}{(x^2+1)^2}=0\\&\\&x^2=1\\&\\&x=\pm 1\\&\\&\text{calculamos la derivada segunda para ver si son máximos o mínimos}\\&\\&f''(x)=\frac{-2x(x^2+1)^2-(-x^2+1)2(x^2+1)2x}{(x^2+1)^4}=\\&\\&\frac{-2x(x^2+1)-4x(-x^2+1)}{(x^2+1)^3}=\frac{-2x^3-2x+4x^3-4x}{(x^2+1)^3}=\\&\\&\frac{2x^3-6x}{(x^2+1)^3}\\&\\&f''(-1)= \frac{-2+6}{8}=\frac 12>0\implies \text{mínimo}\\&\\&f(-1)=\frac{-1}{(-1)^2+1}= -\frac 12\\&\\&\text{Luego }\left(-1,-\frac 12\right) \text{es mínimo}\\&\\&\\&\\&f''(1) = \frac{2-6}{8}=-\frac 12\lt 0\implies \text{máximo}\\&\\&f(1)=\frac{1}{1^2+1}= \frac 12\\&\\&\text{Luego }\left(1,\frac 12\right) \text{es máximo}\\&\\&\text{Como x=-1 es minimo antes decrece luego crece}\\&\text{Como x=1 es máximo antes crece después decrece}\\&\\&(-\infty,-1)\text{ decreciente}\\&(-1, 1) \text{ creciente}\\&(1,+\infty)\text{ decreciente}\\&\\&\\&\text{Ahora puntos de inflexión, donde }f''(x)=0\\&\\&\frac{2x^3-6x}{(x^2+1)^3}=0\implies2x^3-6x=0\\&\\&x^3-3x=0\\&x(x^2-3)=0\\&x(x+\sqrt 3)(x- \sqrt 3)=0\\&\\&x_1=-\sqrt 3,\;x_2=0,\;x_3=\sqrt 3\\&\\&\text{Les calculamos el valor de la función y son}\\&\left(-\sqrt 3,\frac{-\sqrt 3}{4}\right),\quad(0,0),\quad \left(\sqrt 3,\frac{\sqrt 3}{4}\right)\\&\\&\\&En \;(-\infty,-\sqrt 3)\quad f''(-2)=\frac{-16+12}{5^3}\lt0\implies\text{concava hacia abajo}\\&\\&En \;(-\sqrt 3,0)\quad f(-0.5)=\frac{2(-0.5)^3+6·0.5}{\text{algo positivo}}\gt 0\implies\text{concava hacia arriba}\\&\\&En \;(0,\sqrt 3)\quad f(0.5)=\frac{2(0.5)^3-6·0.5}{\text{algo positivo}}\lt 0\implies\text{concava hacia abajo}\\&\\&En \;(\sqrt 3,\infty)\quad f''(2)=\frac{16-12}{5^3}\gt0\implies\text{concava hacia arriba}\\&\end{align}$$Y esta es la gráfica, en azul los máximos o mínimos y en verde los puntos de inflexión.
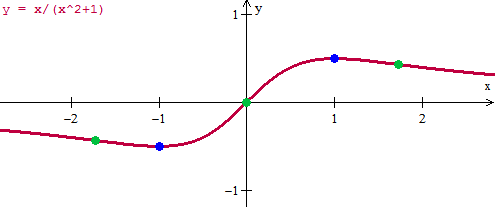
Y eso es todo, como ves es fácil pero lleva mucho trabajo. Manda la otra en otra pregunta.
Saludos.
:
: