Ejercicios de inecuaciones, con procedimiento

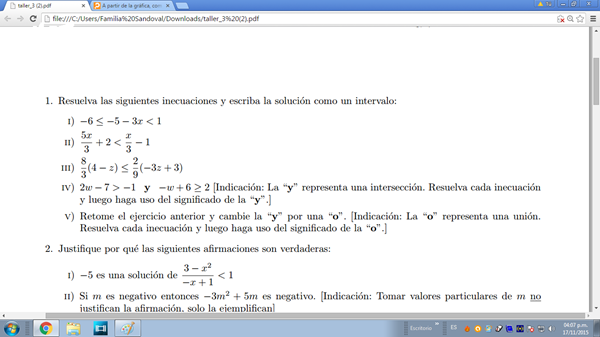
Son muchos ejercicios para una sola pregunta... te dejo la primera parte

$$\begin{align}&I)-6 \le -5-3x<1\ (sumo\ 5...)\\&-1 \le -3x<6\ (divido\ por\ 3...)\\&-1/3 \le -x<2\ (multiplico\ por\ -1\ (invierto \ signos))\\&1/3 \ge x>-2\\&x \in (-2,1/3]\\&II) \frac{5x}{3}+2 <\frac{x}{3}-1 \ (pasaje\ de\ términos...)\\&\frac{5x}{3}-\frac{x}{3}<-1-2 \ (agrupo...)\\&\frac{4x}{3}<-3 \ (multiplico\ por\ 3/4...)\\&x < -3 \cdot \frac{3}{4}\\&x<-\frac{9}{4}\\&x \in (-\infty,-9/4)\\&III)\frac{8}{3}(4-z) \le \frac{2}{9}(-3z+3)\\&(4-z) \le \frac{2}{9}(-3z+3)\cdot \frac{3}{8}\\&4-z \le \frac{1}{12}(-3z+3)\\&4-z \le -\frac{z}{4}+\frac{1}{4}\\&4-\frac{1}{4} \le -\frac{z}{4}+z\\&\frac{15}{4} \le \frac{3}{4}z\\&\frac{15}{4} \cdot \frac{4}{3} \le z\\&5 \le z\\&x \in [5,+\infty)\\&IV) 2w-7 > -1 \land -w+6 \ge2\\&2w-7 > -1\\&2w >6\\&w > 3 \Rightarrow w \in (3,+\infty)\\&-w+6 \ge2\\&-w \ge -4\\&w \le4 \Rightarrow w \in (-\infty,4]\\&\therefore \\&w \in (3,+\infty) \cap w \in (-\infty,4] \Rightarrow w \in (3,4]\\&V)\\&w \in (3,+\infty) \cup w \in (-\infty,4] \Rightarrow w \in (-\infty,+\infty) \text{ (o dicho de otro modo: } w \in R)\end{align}$$