Necesito Graficar: Y= X² + 6 es de matematicas

Es una parábola así que lo que debes hacer (si lo hacés a mano) es encontrar el vértice pues luego la función será simétrica respecto a este eje.

y' = 2x

y'=0 entonces x = 0

y(0) = 0^2 + 6 = 6

o sea que la función es simétrica respecto al eje "Y" (x=0)

Si lo vas a hacer a mano, ahora conviene generar algunos valores para armar una tabla, sabiendo que es simétrico. Lamentablemente esta página no es muy buena para insertar tablas, pero veamos

x = 0 | y=6

x = 1 | y = 7 (como es simétrico respecto a cero, x=-1 también hace y=7)

x = 2 | y = 10 (x=-2 también)

x = 3 | y = 15

Etc

Te dejo una imagen de la función hecha con Geogebra que es un sofware bastante simple de usar (aunque obviamente para el examen no te va a servir)

A la hora de graficar funciones es interesante que sigas los siguientes pasos:

1. Estudiar el dominio:

En este caso se trata de una parábola por lo que

$$\begin{align}&Domf(x)=\mathbb{R}\end{align}$$

2. Puntos de corte con los ejes:

La parábola corta al eje X cuando y=0:

$$\begin{align}&y=0 \Rightarrow x^2+6=0\\\\&x^2=-6\Rightarrow x=\sqrt{-6}= \nexists\end{align}$$

Por tanto y no corta al eje X.

La parábola corta al eje Y cuando x = 0:

$$\begin{align}&y=(0)^2+6=0 \Rightarrow Punto\;de\;corte\;en\;(0,6)\end{align}$$

3. Estudiar máximos, mínimos y crecimiento:

Para estudiar la presencia de extremos relativos (máximos o mínimos) calculamos la primera derivada de y e igualamos a 0. Los valores de x que anulan la primera derivada son extremos relativos:

$$\begin{align}&y'=2x=0 \Rightarrow x=0\;(extremo\;relativo)\end{align}$$

Para comprobar si es un máximo o un mínimo estudiamos el signo de la primera derivada a la derecha y a la izquierda de x=0:

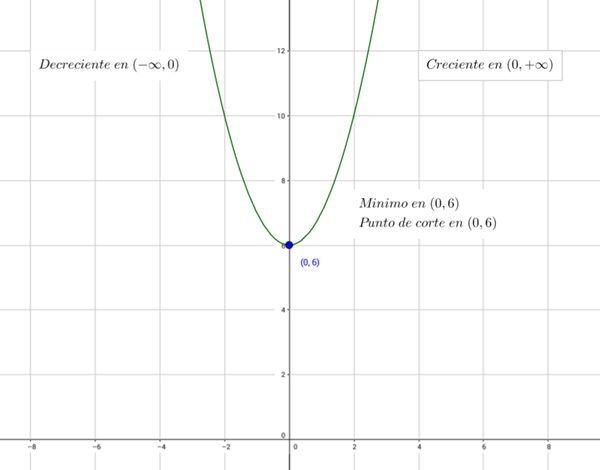
$$\begin{align}&En\;x=-1\::y'=2.-1=-2<0 \Rightarrow Decreciente\;en\;(-\infty,0)\\\\&En\;x=1\::y'=2.1=2>0 \Rightarrow Creciente\;en\;(0,+\infty)\end{align}$$

Al pasar de decreciente a creciente, en x = 0 hay un mínimo. Sus coordenadas son:

$$\begin{align}&x=0 \Rightarrow y=(0)^2+6=6\\\\&Hay\;un\;minimo\;en\;(0,6)\end{align}$$

Ha dado la casualidad de que coinciden el punto de corte con el eje Y con el mínimo de la función.

Con los datos recopilados hasta ahora es suficiente para graficar la función: