Aplicación de la trigonometria al calculo de distancias
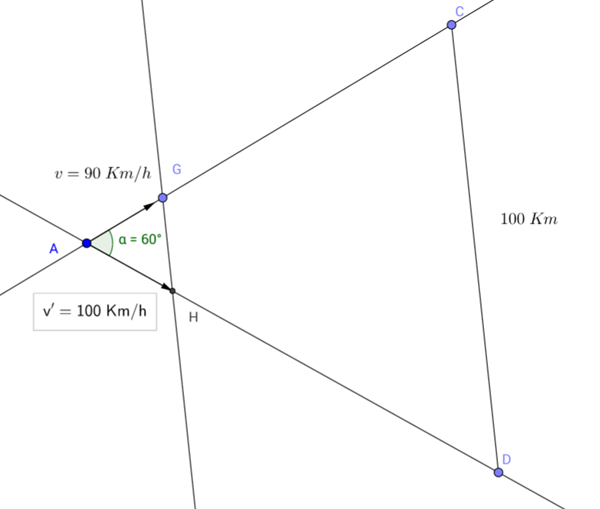
Dos amigos parten en coche de un mismo punto en direcciones que forman un ángulo de 60. Uno viaja a 90 km/h y el otro a 100 km/h. En sus coches llevan un walkie-talkie que tiene un radio de alcance de 100 Km. ¿Durante cuánto tiempo podrán mantener el contacto?
2 Respuestas
Respuesta de javiabelo abelo
1
Respuesta de Valero Angel Serrano Mercadal
1