Diagrama de ven y probabilidad conteo

Te dejo un diagrama con los datos conocidos

Además, sabemos que:

$$\begin{align}&a+d+e+58=92 \to a+d+e=34\\&b+d+f+58=85 \to b+d+f =27\\&c+e+f+58=70 \to c+e+f=12\\&a+b+c+d+e+f+58+2=100 \to  a+b+c+d+e+f=40 \ \text{(El total es el 100%)}\\&\text{Sumo las tres primeras ecuaciones}\\&a+b+c+2d+2e+2f=73 \to d+e+f=33\\&De\ 1) \ d+e=34-a\\&34-a+f= 33 \to a = f+1\\&De\ 2)\ d+f=27-b\\&27-b +e=33 \to e=b+6\\&De\ 3)\ e+f=12-c\\&d+12-c=33 \to d = c+21\end{align}$$

y hasta acá llego, creo que falta algún dato más para poder calcular todas las incógnitas ya que tenemos más incógnitas que ecuaciones.

Hola ;

Mira este es otro razonamiento similar pero me sale 7%

¿

Podría darme su opinión?

Mire a qui esta el razonamiento es muy parecido a el de la imagen solo que tome mal puse 55 en lugar de 58,,,, pero al corregir eso también da 7% .... me gustaría saber si es correcto o los dos nos equivocamos ......espero su respuesta 

Inicia razonamiento 

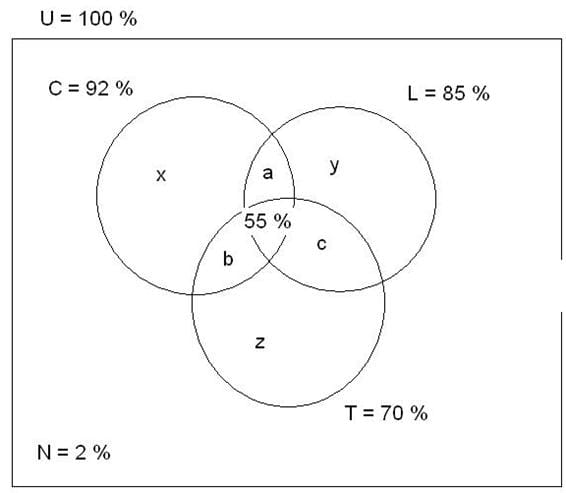
El conjunto C representa a los que tienen teléfono celular; el conjunto L, los que tienen laptop y el conjunto T los que tienen tablet. La N representa a los que no tienen aparato alguno. 

Las variables que están dentro del conjunto significan:  (ver al final diagrama)
x: los que tienen sólo celular 
y: los que tienen sólo laptop 
z: los que tienen sólo tablet 
a: los que tienen celular y laptop 
b: los que tienen celular y tablet 
c: los que tienen laptop y tablet 
Se desea saber cuánto es x + y + z, para ello se construyen estas ecuaciones: 
a + b + x + 55 % = 92 % 
Se refiere a los que tienen celular y laptop (a) más los que tienen celular y tablet (b) + los que tienen sólo celular (c) más los que tienen los tres aparatos, que es igual al 92 % que tienen celulares. 
Esta ecuación se puede escribir en forma reducida: 
(1) a + b + x = 37 % 
Lo mismo se hace con las otras ecuaciones: 
(2) a + c + y = 30 % [85 - 55] 
(3) b + c + z = 15 % [70 - 55] 
La suma de las 3 ecuaciones da: 
a + b + x = 37 % 
a + c + y = 30 % 
b + c + z = 15 % 
-------------------------- 
2 (a + b + c) + x + y + z = 82 ... (4) 
Se requiere saber cuánto es la suma de a + b + c para poder despejar la suma de x + y + z, la cual continúa en los siguientes párrafos. 
El universo U de alumnos encuestados es 100 %, que está formado así: 
x + y + z + a + b + c + 55 + 2 = 100 
Tal ecuación se reduce a: 
x + y + z + a + b + c = 43 ... (5) 
Ahora se desdobla la ecuación 4 para hacer la sustitución: 
a + b + c + a + b + c + x + y + z = 82 
Como se ve en la anterior, las últimas 6 variables del lado izquierdo es igual a las de la ecuación 5, por lo tanto se sustituye el valor de la 5 en ésta y se reduce: 
a + b + c + 43 = 82 
a + b + c = 39 
Esta suma se sustituye en la ecuación 4 para averiguar la suma de x + y + z, que representa a las personas que tienen un solo aparato: 
2 * 39 + x + y + z = 82 
78 + x + y + z = 82 
x + y + z = 4 % 
Respuesta a ambas preguntas: El 4 % de los encuestados tienen un sólo aparato.

mil gracias por su apoyo 

Eso ya es directamente otra pregunta. Te pido que formules una nueva pregunta con este enunciado ya que no tiene nada que ver con el ejercicio inicial de esta pregunta