¿Cómo determinar una función radical cuadrática?

·

·

¡Hola Francisco!

Supongo que será heciendo un estudio general de la función.

Primero veamos el dominio. Para que la función esté definida lo de dentro de la raíz sebe ser no negativo

x^2 - x -2 >= 0

(x-2)(x+1)=0

Sera positiva cuando los dos factores sean positivos o los dos negativos, para que sean positivos

x -2 >=0   ==> x >= 2

x+1 >=0   ==> x >=-1

Se cumplen ambas si

x >=-2

y los dos serán negativos si

x-2<=0  ==> x <=2

x + 1<=0  ==>  x <= -1

se cumplen ambas si x<=-1

Luego Dom f = (-inf, -1) U (2,inf)

·

El rango es Rango f =[0, inf)

Ya que por ser una raíz cuadrada es siempre no negativa, hemos visto que vale 0 en dos puntos y el límite en los infinitos es +infinito

·

Es continua en todo su dominio por ser composición de funciones continuas.

·

Los cortes con el eje X ya vimos que son x=-1 y x=2

Con el eje Y no tiene ya que x=0 no pertenece al dominio de la función

·

No tiene asíntotas verticales ya que la función no tiende a infinito en un punto finito.

No tiene asíntotas horizontales porque el límite en infinito no es finito.

Tiene asíntotas oblicuas porque

$$\begin{align}&m=\lim_{x\to \pm \infty} \frac{f(x)}{x}=\lim_{x\to \pm \infty} \frac{\sqrt{x^2-x-2}}{x}=\\&\\&\lim_{x\to \pm \infty} \pm \sqrt{\frac{x^2-x-2}{x^2}}=\\&\\&\lim_{x\to \pm \infty}\pm \sqrt{1-\frac 1x-\frac 1{x^2}}=\\&\\&\pm \sqrt{1-0-0}=\pm 1  \quad \text{Es finito y distinto de 0}\\&\\&Si\;x\to +\infty \implies m=1\\&\\&Si \;x\to -\infty \implies m=-1\\&\\&\\&\\&b= \lim_{x\to\pm \infty} (f(x)-mx)=\lim_{x\to \pm\infty}(\sqrt{x^2-x-2}\mp x)=\\&\\&\lim_{x\to\pm \infty}\frac{(\sqrt{x^2-x-2}\mp x)(\sqrt{x^2-x-2}\pm x)}{\sqrt{x^2-x-2}\pm x}=\\&\\&\lim_{x\to \pm\infty}\frac{x^2-x-2-x^2}{\sqrt{x^2-x-2}\pm x}=\\&\\&\lim_{x\to \pm\infty}\frac{-x-2}{\sqrt{x^2-x-2}\pm x}=\\&\\&\lim_{x \to \pm \infty} \frac{-1-\frac 2x}{\pm \sqrt{1-\frac 1x-\frac 2{x^2}}\pm1}=\frac{-1}{\pm 2}=\mp \frac 12\\&\\&\text {Si }x\to +\infty \implies b=-\frac 12\\&\\&\text{Si }x\to -\infty \implies b =\frac 12\\&\\&\text {Luego las asíntotas oblicuas son}\\&\\&Si\;x\to+\infty\implies y= x-\frac 12\\&\\&Si\;x\to-\infty\implies y= -x+\frac 12\\&\\&\\&\\&\end{align}$$

·

La derivada es:

$$\begin{align}&f'(x)=\frac{2x-1}{2 \sqrt{x^2-x-2}}\\&\\&2x-1=0\\&\\&x=\frac 12\\&\\&\text como \frac 12\notin Dom f \implies \text{ no hay máximos-mínimos relativos}\\&\\&\text{Vimos que había minimos absolutos en x=-1 y x=2}\\&\\&Si\; x\lt \frac 12 \implies f'(x)\lt 0\implies \text{decreciente en }(-\infty, -1)\\&\\&Si\;x\gt \frac 12 \implies f'(x)\gt0\implies \text{creciente en }(2,\;\infty)\end{align}$$

Te dejo que hagas la derivada segunda, el resultado  es

$$\begin{align}&\frac {-9}{4 \sqrt{(x^2-x-2)^3}}\end{align}$$

Por lo cual no hay puntos de inflexión y es siempre cóncava hacia abajo.

Y la gráfica es esta:

:

:
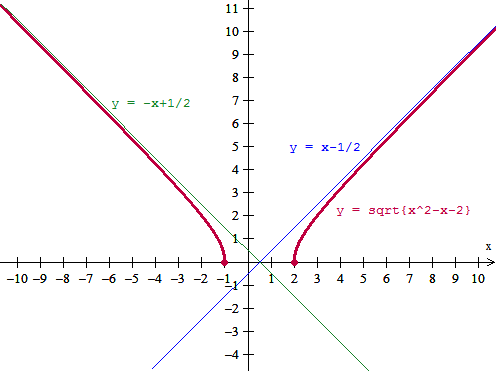